
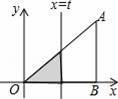
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.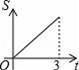
 B.
B.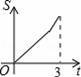
 C.
C.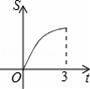
 D.
D.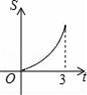

D【考点】二次函数的图象.
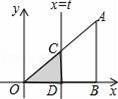
【分析】Rt△AOB中,AB⊥OB,且AB=OB=3,所以很容易求得∠AOB=∠A=45°;再由平行线的性质得出∠OCD=∠A,即∠AOD=∠OCD=45°,进而证明OD=CD=t;最后根据三角形的面积公式,解答出S与t之间的函数关系式,由函数解析式来选择图象.
【解答】解:∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=
 ×OD×CD
×OD×CD
=
 t2(0≤t≤3),即S=
t2(0≤t≤3),即S=
 t2(0≤t≤3).
t2(0≤t≤3).
故S与t之间的函数关系的图象应为定义域为[0,3]、开口向上的二次函数图象;
故选D.

【点评】本题主要考查的是二次函数解析式的求法及二次函数的图象特征.


科目:初中数学 来源: 题型:
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款.已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等,如果设第一次捐款人数是x人,那么x满足的方程是( )
A.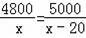
 B.
B.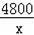
 =
=

C.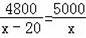
 D.
D.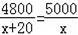

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
 ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)


查看答案和解析>>
科目:初中数学 来源: 题型:
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )


A.(10π﹣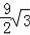
 )米2 B.(π﹣
)米2 B.(π﹣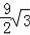
 )米2 C.(6π﹣
)米2 C.(6π﹣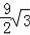
 )米2 D.(6π﹣
)米2 D.(6π﹣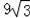
 )米2
)米2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com