
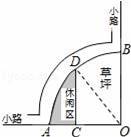
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )


A.(10π﹣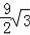
 )米2 B.(π﹣
)米2 B.(π﹣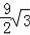
 )米2 C.(6π﹣
)米2 C.(6π﹣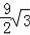
 )米2 D.(6π﹣
)米2 D.(6π﹣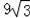
 )米2
)米2
C【考点】扇形面积的计算.
【专题】压轴题;探究型.
【分析】先根据半径OA长是6米,C是OA的中点可知OC=
 OA=3,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD﹣S△DOC即可得出结论.
OA=3,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD﹣S△DOC即可得出结论.
【解答】解:连接OD,
∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=
 OA=
OA=
 ×6=3米,
×6=3米,
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,
∵OD=6,OC=3,
∴CD=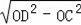
 =
=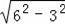
 =3
=3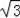
 米,
米,
∵sin∠DOC=
 =
=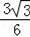
 =
=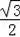
 ,
,
∴∠DOC=60°,
∴S阴影=S扇形AOD﹣S△DOC=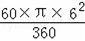
 ﹣
﹣
 ×3×3
×3×3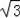
 =(6π﹣
=(6π﹣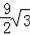
 )平方米.
)平方米.
故选C.

【点评】本题考查的是扇形的面积,根据题意求出∠DOC的度数,再由S阴影=S扇形AOD﹣S△DOC得出结论是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
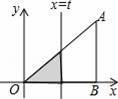
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.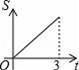
 B.
B.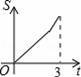
 C.
C.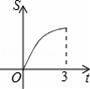
 D.
D.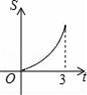

查看答案和解析>>
科目:初中数学 来源: 题型:
(1)数学课上,老师出了一道题,如图①,Rt△ABC中,∠C=90°,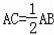
 ,求证:∠B=30°,请你完成证明过程.
,求证:∠B=30°,请你完成证明过程.
(2)如图②,四边形ABCD是一张边长为2的正方形纸片,E、F分别为AB、CD的中点,沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,折痕交AE于点G,请运用(1)中的结论求∠ADG的度数和AG的长.
(3)若矩形纸片ABCD按如图③所示的方式折叠,B、D两点恰好重合于一点O(如图④),当AB=6,求EF的长.
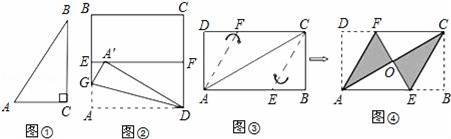

查看答案和解析>>
科目:初中数学 来源: 题型:
某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数y=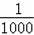
 x2+
x2+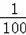
 x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
查看答案和解析>>
科目:初中数学 来源: 题型:
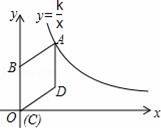
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
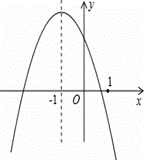
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论:
① abc<0 ② 4ac-b2<0 ③ 4a+c<2b ④ 3b+2c<0
⑤ m(am+b)+b<a(m≠-1)
其中正确的结论是 (把所有正确的结论的序号都填写在横线上)
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com