
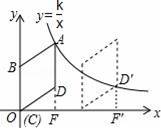
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
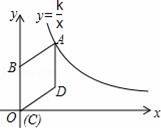

【考点】反比例函数综合题.
【分析】(1)过点D作x轴的垂线,垂足为F,首先得出A点坐标,再利用反比例函数图象上点的坐标性质得出即可;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数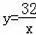
 (x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
(x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
【解答】解:(1)过点D作x轴的垂线,垂足为F,
∵点D的坐标为(4,3),
∴OF=4,DF=3,
∴OD=5,
∴AD=5,
∴点A坐标为(4,8),
∴k=xy=4×8=32,
∴k=32;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数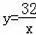
 (x>0)的图象D′点处,
(x>0)的图象D′点处,
过点D′做x轴的垂线,垂足为F′.
∵DF=3,
∴D′F′=3,
∴点D′的纵坐标为3,
∵点D′在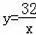
 的图象上
的图象上
∴3=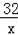
 ,
,
解得:x=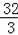
 ,
,
即OF′=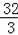
 ,
,
∴FF′=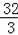
 ﹣4=
﹣4=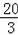
 ,
,
∴菱形ABCD平移的距离为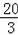
 .
.

【点评】此题主要考查了反比例函数综合以及反比例函数图象上点的坐标性质,得出A点坐标是解题关键.


科目:初中数学 来源: 题型:
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
 ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)


查看答案和解析>>
科目:初中数学 来源: 题型:
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )


A.(10π﹣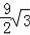
 )米2 B.(π﹣
)米2 B.(π﹣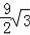
 )米2 C.(6π﹣
)米2 C.(6π﹣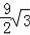
 )米2 D.(6π﹣
)米2 D.(6π﹣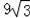
 )米2
)米2
查看答案和解析>>
科目:初中数学 来源: 题型:
为了估计某市空气质量情况,某同学在30天里做了如下记录:
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 6 | 5 | 1 |
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为 天.
查看答案和解析>>
科目:初中数学 来源: 题型:
一个三角形满足一个角是另一个角的3倍,那么我们称这个三角形是
“智慧三角形”,下列各组数据中,能作为一个智慧三角形的三边长的
一组是( )
A、1,2,3 B、1,1,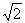 C、1,1,
C、1,1,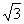 D、1,2,
D、1,2,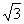
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com