练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知二次函数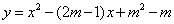（m是常数，且）.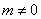

    （1）证明：不论m取何值时，该二次函数图象总与x轴有两个交点；

    （2）若A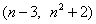、B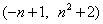是该二次函数图象上的两个不同点，求二次函数解析式和n的值；

    （3）设二次函数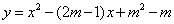与x轴两个交点的横坐标分别为x1、x2（其中x1＞ x2），若p是关于m的函数，且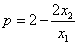，请结合函数的图象回答：当p <m时，求m的取值范围.


    （1）∵

    ∴△=＞0

    ∴不论m为何值时,该二次函数与x轴有两个交点        4分

     (2) ∵由A,B两点知对称轴为:直线x= -1

    ∴，m=,∴

    代入A(n-3, ),    得n=7/16      4分

    (3) ∵

    ∴  ∴ x1=m,   x2=m-1

    ∵P=   ∴P=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    抛物线的对称轴是直线x=1.5,且图象过点A(0, ﹣4)和点B（4，0）,

    （1）求抛物线的解析式；

    （2）若抛物线与x轴的另一个交点为C，M是线段BC上的任意一点，当△MAB为等腰三角形时，求M点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，BC=18，AC=12，AB=9，点D，E分别是直线AB，AC上的两个点，AE=4.

    若由A，D，E构成的三角形与△ABC相似，则DB的长为                    

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=ax2 +bx+c（a，b，c为常数，a＜0）的图象经过点（﹣1，1），（4，﹣4）.下列结论：①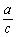＜0；

              ②当x＞1时，y的值随x值的增大而减小；

              ③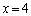是方程ax2+（b+1）x+c=0的一个根；

              ④当﹣1＜x＜4时，ax2+（b+1）x+c＞0．其中正确的是(     )

    A、①③        B、①②④        C、①③④         D、②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知△ABC．

    （1）用直尺和圆规作出⊙O，使⊙O经过A，C两点，且圆心O在AB边上．（不写作法，保留作图痕迹）

    （2）若∠CAB＝22.5°,∠B＝45°且⊙O的半径为1，

    试求出AB的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知4个数据：，，，，其中，是方程的两个根，则这4个数据的中位数是（      ）   A.1             B.             C.2           D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从-2，-8，5中任取两个不同的数作为点的坐标，该点在第三象限的概率为       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    估算的值是在……………………………………………………………【      】

    A. 5和6之间     B. 6和7之间    C. 7和8之间    D. 8和9之间

    查看答案和解析>>

    科目：初中数学 来源： 题型：


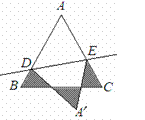
     如图，等边ΔABC的边长为cm,D、E分别是AB、AC上的点，将

    ΔABC沿直线DE折叠，点A落在A′处，且A′在ΔABC外部，则阴影

    部分图形的周长为（　）cm.

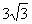    A. 　　　B.   　　C.     D.

    查看答案和解析>>

    同步练习册答案