
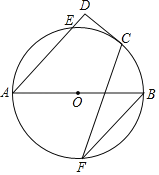
【题目】如图,点C在以AB为直径的⊙O上.AE与过点C的切线垂直,垂足为D,AD交⊙O于点E,过B作BF∥AE交⊙O于点F,连接CF.
(1)求证:∠B=2∠F;
(2)已知AE=8,DE=2,过B作BF∥AE交⊙O于F,连接CF,求CF的长.
【答案】(1)证明见解析;(2)CF=2![]() .
.
【解析】
(1)连接OC,根据切线的性质得出OC⊥CD,即可证得OC∥AD,根据平行线的性质以及等腰三角形的性质得出∠DAB=2∠F,进而即可证得结论;
(2)连接AF、AC,延长CO交⊙O于H,过O作OG⊥AE于G,首先根据平行线的性质证得∠ACH=∠HCF然后根据垂径定理证得AH=FH,根据垂直平分线的性质得出AC=FC,进而通过证得四边形OCDG是矩形求得半径,然后根据勾股定理求得OG.得出CD,最后根据勾股定理求得AC,从而求得FC.
(1)证明:连接OC,
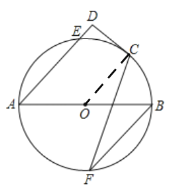
∵CD是⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD,
∴∠BOC=∠DAB,
由圆周角定理得,∠BOC=2∠F,
∴∠DAB=2∠F,
∵AD∥BF,
∴∠B=∠DAB,
∴∠B=2∠F;
(2)解:连接AF、AC,延长CO交⊙O于H,过O作OG⊥AE于G,
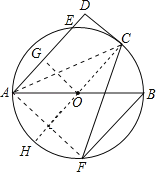
∵OC∥AD,AE∥BF,
∴OC∥BF,
∴∠F=∠HCF,
∵∠B=2∠F,
∴∠B=2∠HCF,
∵∠ACF=∠B,
∴∠ACF=2∠HCF,
∴∠ACH=∠HCF,
∴![]() ,
,
∴CH垂直平分AF,
∴CF=AC,
∵OG⊥AE,
∴AG=EG=![]() 4,
4,
∴GD=GE+ED=4+2=6,
∵∠OGD=∠D=∠OCD=90°,
∴四边形OCDG是矩形,
∴OC=GD=6,OG=CD,
∵OA=OC=6,AG=4,
∴OG=![]()
∴DC=![]() ,
,
在Rt△ADC中,AC=![]()
∴CF=AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
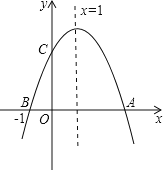
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖家经营着一家水果店,在杨梅旺销季节,她的父母经常去果园采购杨梅用于销售.果园的杨梅价格如下:购买数量不超过20筐,每筐进价20元;购买数量超过20筐,每筐进价18元.小颖在观察水果店一段时间的销售情况后发现,当杨梅的售价为每筐30元时,每天可销售30筐;每筐售价提高1元,每天销量减少1筐;每筐售价降低1元,每天销量增加1筐.若每天购进的杨梅能全部售出,且售价不低于进价,从果园进货的运费为每天100元.
(1)设售价为每筐![]() 元,则每天可售出___________筐.
元,则每天可售出___________筐.
(2)当每筐杨梅的售价定为多少元时,杨梅的日销售利润最大?最大日利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
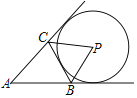
A.8B.10C.13D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
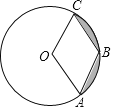
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
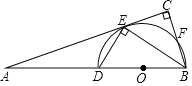
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点F,且E为弧DF的中点.
(1)求证:AC是半圆O的切线;
(2)若BC=8,BE=6![]() ,求半径的长.
,求半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com