
【题目】如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E. 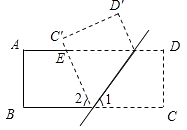
(1)若∠1=62°,则∠2=
(2)试判断△EMN的形状,并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
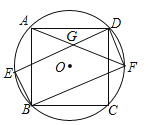
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①平分弦的直径垂直于弦.②半圆所对的圆周角是直角.③一条弧所对的圆周角等于它所对的圆心角的一半.④在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.⑤圆内接平行四边形是矩形.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面图形上的任意两点P,Q,如果经过某种变换(如:平移、旋转、轴对称等)得到新图形上的对应点P′,Q′,保持P P′= Q Q′,我们把这种对应点连线相等的变换称为“同步变换”。对于三种变换: ①平移、②旋转、③轴对称,其中一定是“同步变换”的有(填序号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件中:
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
能判定AB∥CD的条件个数有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com