Question

【题目】如图，在平面直角坐标系中，直线（）与直线平行，且与直线交于点.

（1）求直线的函数表达式；

（2）、分别是直线、上两点，点的横坐标为，且轴，若，求的值.

Answer 1

【答案】（1）；（2）的值是-1或3.

【解析】

（1）先利用直线的解析式求出a的值，再根据直线与直线平行求出k的值，最后将点M的坐标代入的解析式可求出b的值，从而可得直线的函数表达式；

（2）由图可知，需分点D、E在点M的左侧和右侧两种情况分析，设点D、E的坐标，根据建立等式求解即可.

（1）把代入

得到

与直线平行

把代入直线中

得到，解得

故直线的函数表达式为；

（2）因轴，所以点D和点E的横坐标相同，

由直线和的解析式，可设，

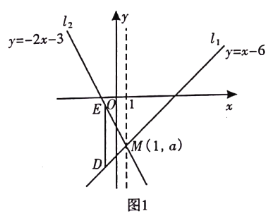
由图可知，需分点D、E在点M的左侧和右侧两种情况：

①如图1，当点D、E在点M的左侧，即时，

∵，

∴，

解得；

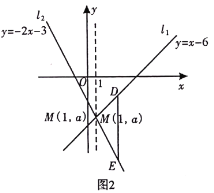
②如图2，当点D、E在点M的右侧，即时，

∵，

∴，

解得，

综上所述，的值是-1或3.