
分析 根据非负数的性质判断出反比例函数图象位于第一、三象限,再根据交点坐标判断出二次函数图象开口向上且对称轴在y轴左边,然后写出二次函数图象在反比例函数图象上方部分的x的取值范围即可.
解答 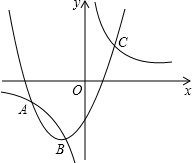 解:∵k2>0,
解:∵k2>0,
∴反比例函数图象位于第一、三象限,
∵抛物线与双曲线交点为A(-4,m)、B(-2,n)、C(3,p).
∴抛物线开口向上且对称轴在y轴左边,如图所示,
x>0时,不等式两边同除以x并移项得,ax2+bx+c>$\frac{{k}^{2}}{x}$,
所以,不等式的解集是x>3,
x<0时,不等式两边同除以x并移项得,ax2+bx+c<$\frac{{k}^{2}}{x}$,
所以,不等式的解集是-4<x<-2,
综上所述,不等式的解集是0<x<3或-4<x<-2.
故答案为:x>3或-4<x<-2.
点评 本题考查了二次函数与不等式,熟练掌握反比例函数与二次函数图象的性质是解题的关键,要注意根据x的取值范围分情况讨论,作出图形更形象直观.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
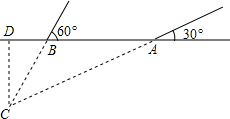 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.
2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{x{y}^{2}}{5}$的系数是-5 | B. | $\frac{t}{2}$是分式 | ||
| C. | $\frac{\sqrt{2}}{2}$不是分数 | D. | -22xyz2的次数是6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P站东70千米 | B. | P站东10千米 | C. | P站西10千米 | D. | P站西70千米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com