如图所示，在⊙O中， 
，弦AB与弦AC交于点A，弦CD与AB交于点F，连接BC．
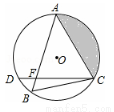
（1）求证：AC2=AB•AF；
（2）若⊙O的半径长为2cm，∠B=60°，求图中阴影部分面积．
学练快车道快乐假期寒假作业系列答案科目：初中数学 来源：2014-2015学年重庆市巴南区九年级下学期期中质量监测数学试卷（解析版） 题型：填空题
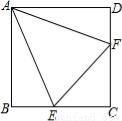
如图，正方形ABCD中，E、F分别为BC、CD上的点，若BE=3，DF=2且∠EAF=45°，则EF= ．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级学业水平模拟数学试卷（解析版） 题型：选择题
某商场的老板销售一种商品，他要以不低于进价l5％的价格才能出售，但为了获得更多利润，他以高出进价80％的价格标价．若这种商品标价为360元，你最多讲多少价（降价多少元）时商店老板才能出售
A．120元 B．130元 C．140元 D．150元
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级中考适应性测试四数学试卷（解析版） 题型：解答题
如图，在平面直角坐标系中，已知OA=2，OC=4，⊙M与
轴相切于点C，与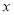
轴交于A，B两点，∠ACD=90°，抛物线
经过A，B，C三点．
（1）求证：∠CAO=∠CAD；
（2）求弦BD的长；
（3）在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级中考适应性测试四数学试卷（解析版） 题型：填空题
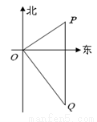
小明在某风景区的观景台O处观测到东北方向的P处有一艘货船, 该船正向南匀速航 行30分钟后再观察时,该船已航行到O的南偏东30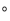
,且与O相距6km的Q处．如图所示．货船的航行速度是____________km/h．（结果用根号表示．）
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级中考适应性测试四数学试卷（解析版） 题型：选择题
已知关于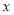
的方程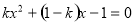
，下列说法正确的是
A．当
时，方程无解
B．当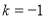
时，方程有两个相等的实数解
C．当
时，方程有一个实数解
D．当
时，方程总有两个不相等的实数解
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：解答题
【课本节选】
反比例函数y= （k为常数,k≠0）的图象是双曲线.当k＞0时，双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y=（k＞0）的增减性来进行说理．如图，当x＞0时．
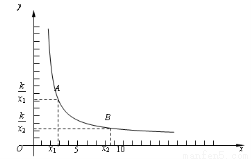
在函数图象上任意取两点A、B，设A（x1，），B（x2，），
且0＜x1＜ x2．
下面只需要比较和的大小．
—= ．
∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．
∴＜0．即＜ ．
这说明：x1＜ x2时，＞．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．
同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y= （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax2 （a＞0，a为常数）的对称性和增减性，并进行说理．
对称性： ；
增减性： ．
说理：
（3）对于二次函数y=ax2＋bx＋c （a＞0，a，b，c为常数），请你从增减性的角度，简要解释为何当x=— 时函数取得最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
中，最小的数是 ( )
B．0 C．
D．
的图象经过点P（
，
）和Q（
，
），则
的值为________．