
����Ŀ�����мס��������������ֱ�װ�н�ˮ�ܺͳ�ˮ�� ���������Ľ���ˮ�ٶȲ��䣬�ȴ��������Ľ�ˮ�ܣ�2����ʱ�ٴ������Ľ�ˮ�ܣ��ֹ�2���ӹرռ������Ľ�ˮ�ܣ��ٹ�4����ͬʱ�������Ľ�����ˮ�ܡ�ֱ��12����ʱ��ͬʱ�ر��������Ľ���ˮ�ܡ��ر�ˮ�ܵ�ʱ����Բ��ơ������е�ˮ��y(��)��������עˮʱ��x(��)֮��Ĺ�ϵ��ͼ��ʾ
��1����������Ľ�����ˮ�ٶȣ�
��2����![]() ʱ������������Ƿ������������ˮ����ȣ������ڣ������ʱx��ֵ��
ʱ������������Ƿ������������ˮ����ȣ������ڣ������ʱx��ֵ��
��3�����������������װһ����ˮ�ܣ����ˮ�ٶ���2�����֣���ʹ��������12����ʱ��ˮ����� ����Ӧ���ڵڼ����Ӵ˽�ˮ�ܣ�
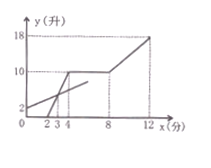
���𰸡���1��5,3����2��8����3��10
��������
��1������ͼʾ֪������������2�����ڽ�ˮ��Ϊ10����
��2����ͼ��֪���������ڵ�3����ʱˮ��Ϊ��5����3-2��=5����������A��3��5������y��=kx+b��k��0�������ô���ϵ������øú�������ʽ����y=10������ֵ����.
��3������t����ʱ�����������������ﵽ18��ʱ�г���ʽ.
(1)�Ľ�ˮ�ٶȣ�![]() =5(��/��)��
=5(��/��)��
�ij�ˮ�ٶȣ�5![]() =3(��/��)��
=3(��/��)��
(2)���ڡ�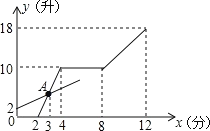
��ͼ��֪,�������ڵ�3����ʱˮ��Ϊ��5��(32)=5(��),��A(3,5).
��y��=kx+b(k��0)��������ã�
3k+b=5��b=2��
��ã�{k=1b=2��
����y��=x+2.
��y��=10ʱ��x=8.
������������ˮ�ܴ�8����ʱ��������ˮ����ȣ�
(3)��x=12ʱ��y��=18.
����t���Ӵ���ˮ��.
����ɵ�,2+12+2(12-t)=18
��t=10.
Ӧ�ڵ�ʮ���Ӵ˽�ˮ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺ ͼ1�DZ߳��ֱ�Ϊa��b��a��b���������ȱ�������ֽƬABC��C��DE������һ��C��C���غϣ���ͼ�Σ�
������֤����
��1���������̶���ABC������C��DE�Ƶ�C��˳ʱ�뷽����ת30�㣬����AD��BE����ͼ2����ͼ2�У��߶�BE��AD֮����������Ĵ�С��ϵ��֤����Ľ��ۣ� 
��2������������ͼ1�еġ�C��DE���Ƶ�C��˳ʱ�뷽��������תһ���ǶȦ�������AD��BE����ͼ3����ͼ3�У��߶�BE��AD֮����������Ĵ�С��ϵ��֤����Ľ��ۣ� 
�����뷢�֣�
��������IJ������̣�������뵱��Ϊ���ٶ�ʱ���߶�AD�ij�������Ƕ��٣�����Ϊ���ٶ�ʱ���߶�AD�ij�����С�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD��EF�ֱ�AB��CD��G��F���㣬����FMƽ�֡�EFD��������FMƽ�ƣ�ʹ�ö˵�F���G�غ��ҵõ�����GN������EFC=110�������AGN�Ķ����ǣ�������

A. 120�� B. 125�� C. 135�� D. 145��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��EF��AB���ڵ�M����CD���ڵ�O��OGƽ�֡�DOF������COM=120�㣬��EMB=![]() ��COF��
��COF��

��1�����FOG�Ķ�����
��2��д��һ�����FOG��Ϊͬλ�ǵĽǣ�
��3�����AMO�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Ӱ�����DZ߳�Ϊa�Ĵ��������м�ȥһ���߳�Ϊb��С�����κ����õ���ͼ�Σ�����Ӱ����ͨ���ƴ���γ��µ�ͼ�Σ���������3�ָ�ƴ�����������ܹ���֤ƽ���ʽ����( )

A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����۵�������С��һ��ij��ֲ�ﻨ�۵�����ԼΪ0.000037���ˣ���֪1��=1000���ˣ���ô0.000037���˿��ÿ�ѧ��������ʾΪ
A. 3.7��10��5�� B. 3.7��10��6�� C. 37��10��7�� D. 3.7��10��8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)��23��![]() (2 018��3)0��
(2 018��3)0��![]() ��(2)
��(2)![]() ��
��
(3)(��2��x)(��2��x)�� (4)(a��b��c)(a��b��c).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ����ֱ������ABCD�У���BAD=90�㣬E��ֱ��AB��һ�㣬��E��ֱ��l��BC����ֱ��CD�ڵ�F����ֱ��l����ƽ�ƣ���ƽ�ƾ���BEΪt��t��0����ֱ������ABCD��ֱ��lɨ���������ͼ����Ӱ���֣�ΪS��S����t�ĺ���ͼ����ͼ����ʾ��OMΪ�߶Σ�MNΪ�����ߵ�һ���֣�NQΪ���ߣ�N�������Ϊ4��
��Ϣ��ȡ
��1�������ϵij�AB=��
��2��ֱ������ABCD�����=��
ͼ������
��3��д��ͼ��������NQ��ʾ��ʵ�����壻
��4����2��t��4ʱ����S����t�ĺ�����ϵʽ��
������
��5����tΪ��ֵʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������
��ͼ��BEƽ����ABD��DEƽ����BDC�������������£�90�㣬��˵����AB��CD.

����������̣�
��BEƽ�֡�ABD(��֪)��
���ABD��2����(__________)��
��DEƽ�֡�BDC(��֪)��
���BDC��2���� (__________)��
���ABD����BDC��2������2������2(����������)( __________)��
�ߡ�����������90��(��֪)��
���ABD����BDC��180��(__________)��
��AB��CD(____________________)��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com