
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��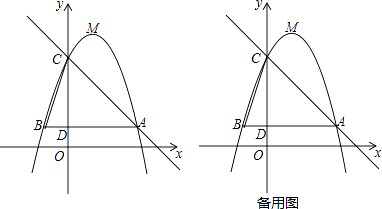
��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ������ڡ�ABC���ڲ�����������ABC�ı߽磩����m��ȡֵ��Χ��
��3����P��ֱ��AC�ϵĶ��㣬����P����C����M�����ɵ����������BCD���ƣ���ֱ��д�����е�P�����ֱ꣨��д�����������д�����̣���
���𰸡�
��1���⣺�ѵ�A��3��1������C��0��4��������κ���y=��x2+bx+c�ã�
![]() ���
��� ![]()
����κ�������ʽΪy=��x2+2x+4��
�䷽��y=����x��1��2+5��
���M��������1��5����
��2���⣺��ֱ��AC����ʽΪy=kx+b���ѵ�A��3��1����C��0��4������ã�
![]() ���
��� ![]()
��ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F
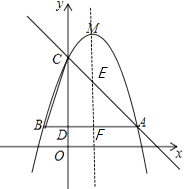
��x=1����ֱ��AC����ʽy=��x+4���y=3�����E����Ϊ��1��3������F����Ϊ��1��1��
��1��5��m��3�����2��m��4
��3���⣺����MC����MG��y�Ტ�ӳ���AC�ڵ�N�����G����Ϊ��0��5��
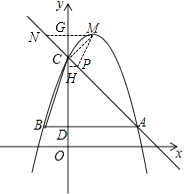
��MG=1��GC=5��4=1
��MC= ![]() =
= ![]() ��
��
��y=5����y=��x+4���x=��1�����N��������1��5����
��NG=GC��GM=GC��
���NCG=��GCM=45�㣬
���NCM=90�㣬
�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ��
�����С�PCM�ס�BDC������ ![]()
��BD=1��CD=3��
��CP= ![]() =
= ![]() =
= ![]() ��
��
��CD=DA=3��
���DCA=45�㣬
����P��y���Ҳ࣬��PH��y�ᣬ
�ߡ�PCH=45�㣬CP= ![]()
��PH= ![]() =
= ![]()
��x= ![]() ����y=��x+4�����y=
����y=��x+4�����y= ![]() ��
��
��P1�� ![]() ����
����
ͬ���ɵã�����P��y����࣬���x=�� ![]() ����y=��x+4�����y=
����y=��x+4�����y= ![]()
��P2�� ![]() ����
����
�����С�PCM�ס�CDB������ ![]()
��CP= ![]() =3
=3 ![]()
��PH=3 ![]() ��
�� ![]() =3��
=3��
����P��y���Ҳ࣬��x=3����y=��x+4�����y=1��
����P��y����࣬��x=��3����y=��x+4�����y=7
��P3��3��1����P4����3��7����
�����з�������õ�P������4�����ֱ�ΪP1�� ![]() ����P2��
����P2�� ![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����
����������1������A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ��2����M�����ŶԳ���ֱ��x=1����ƽ�Ƶģ��������ֱ��AC�Ľ���ʽ����x=1���������M������ƽ��ʱ��AC��AB�ཻʱy��ֵ�����ɵõ�m��ȡֵ��Χ����3������������ɵá�MCP=90�㣬������PCM���BCD���ƣ���Ҫ���з������ۣ��ֳɡ�PCM�ס�BDC���PCM�ס�CDB���֣�Ȼ�����ñߵĶ�Ӧ��ֵ��������꣮
�����㾫����������Ĺؼ������������������ε����ʵ����֪ʶ�����ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��![]() ��
��![]() ��
��![]() ����ͼ��ʽ���У����涨��m��n����ʾ��m�Ŵ������ҵ�n��������7��3������ʾ������__����5��2���루20��17����ʾ������֮����__��
����ͼ��ʽ���У����涨��m��n����ʾ��m�Ŵ������ҵ�n��������7��3������ʾ������__����5��2���루20��17����ʾ������֮����__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬A�������Ϊ![]() ��C�������Ϊ
��C�������Ϊ![]() ����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����
����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����![]() ��·���ƶ�
��·���ƶ�![]() �������ų������ƶ�һ��
�������ų������ƶ�һ��![]() ��
��
![]() ���B������
���B������![]() ______
______![]()
![]() ����P�ƶ���4��ʱ�������ʱP���λ�ã��������P�����꣮
����P�ƶ���4��ʱ�������ʱP���λ�ã��������P�����꣮
![]() ���ƶ������У�����P��x�����Ϊ5����λ����ʱ�����P�ƶ���ʱ�䣮
���ƶ������У�����P��x�����Ϊ5����λ����ʱ�����P�ƶ���ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������У��ȫ���ܵ�ȫ���Ĺ㷺��ע��������жԲ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1������ͳ��ͼ�С������˽⡱��������Ӧ���ε�Բ�Ľ�Ϊ�ȣ��벹ȫ����ͳ��ͼ��
��2�����ﵽ���˽⡱�̶ȵ�������1������2��Ů�����ﵽ�����˽⡱�ij̶ȵ�������1��������1��Ů�������ֱ�Ӵﵽ���˽⡱�̶Ⱥ͡����˽⡱�����зֱ��ȡ1�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�۲���������ͼ 1����ABC �У���ACB=90�㣬AC=BC,ֱ�� L ����C���� A,B ��ֱ�� L ͬ�࣬BD��L�� AE��L������ֱ�ΪD,E
��֤:��AEC�ա�CDB
��2�����̽������ͼ 2��Rt��ABC �У���ACB=90�㣬AC=4����б�� AB �Ƶ� A ��ʱ����ת 90���� AB��, ����B��C������AB��C �����
��3����չ��������ͼ 3���ȱ���EBC ����EC=BC=3cm���� O �� BC ���� OC=2cm������ P �ӵ� E ������EC �� 1cm/s �ٶ��˶������� OP,���߶� OP �Ƶ�O ��ʱ����ת 120���õ��߶� OF����� P �˶���ʱ��Ϊt �롣
��t= ��ʱ��OF��ED


��Ҫʹ��F ǡ����������EB �ϣ����P �˶���ʱ��t
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB=1��AD= ![]() ��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF��EC���ڵ�H�����н����У���AF=FH����BO=BF����CA=CH����BE=3ED����ȷ�ĸ����ǣ� ��
��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF��EC���ڵ�H�����н����У���AF=FH����BO=BF����CA=CH����BE=3ED����ȷ�ĸ����ǣ� �� 
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P����AOB�ı�OB�ϵ�һ�㣬����P��OB�Ĵ��ߣ���OA�ڵ�C��
��1�� ����C��OB��ƽ����CD��
��2�� ����P��OA�Ĵ��ߣ�����ΪH��
��3�� �߶�PH�ij����ǵ�P�� �ľ��룬�߶� �ij����ǵ�C��ֱ��OB�ľ��룮�߶�PC��PH��OC�������߶δ�С��ϵ�� ���á����������ӣ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ʾ�������˴�ͬһ���ص��������������ʮ��ʱ���״�Լ����13ǧ�ף�����ͼ��ش�
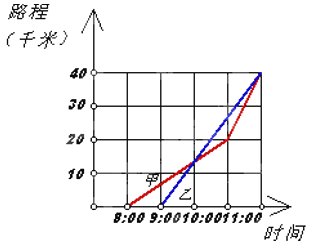
��1�����Ǽ����ӳ�����
��2�����Ǽ����ӳ�������ʮ��ʱ������Լ���˶���ǧ�ף�
��3����ʮ��Ϊֹ���ĸ��˵��ٶȿ죿
��4�����������ڼ�����������
��5�����ܽ�ͼ���еõ���Ϣ�����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com