
【题目】如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AC平分∠BAD,求证:ABCD为菱形.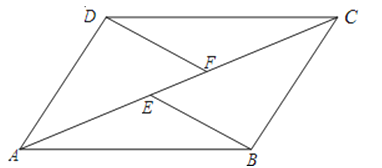
【答案】证明:(1)∵DF∥BE,
∴∠DFA=∠CEB,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ADF和△CBE中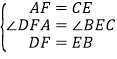 ,
,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAC=∠ACB,
∴AD∥CB,
∴四边形ABCD是平行四边形;
(2)∵AC平分∠BAD,
∴∠DAC=∠BAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴ABCD为菱形.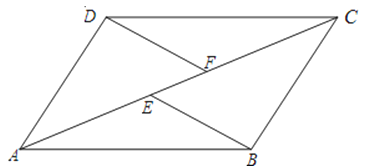
【解析】(1)首先证明△ADF≌△CBE,根据全等三角形的性质可得AD=CB,∠DAC=∠ACB,进而可得证明AD∥CB,根据一组对边平行且等的四边形是平行四边形可得四边形ABCD是平行四边形;
(2)首先根据角平分线的性质可得∠DAC=∠BAC,进而可得出AB=BC,再根据一组邻边相等的平行四边形是菱形可得结论.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形).


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,DE垂直平分AC , DF⊥BC , 当△ABC满足条件时,四边形DECF是正方形.(要求:①不再添加任何辅助线,②只需填一个符合要求的条件)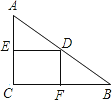
查看答案和解析>>
科目:初中数学 来源: 题型:
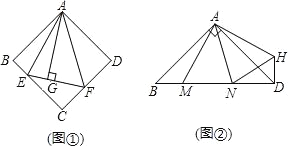
【题目】(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN2,ND2,DH2之间的数量关系,并说明理由.
(3)在图①中,若EG=4,GF=6,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.
(1)写出两个不全等且与△GHC相似的三角形,并任选其中的一个进行证明;
(2)求GH的长.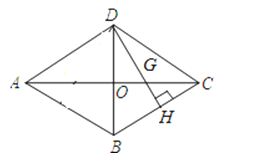
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市某汽车厂生产某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯用电费用26元,已知每行驶1 km,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1 km纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.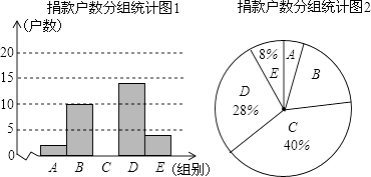
(1)a= , 本次调查样本的容量是;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com