
分析 根据题意知道:张强每小时走这段路程的$\frac{1}{11}$,王丽每小时走这段路程的$\frac{1}{5}$,并且张强比王丽早出发4小时,可以设王丽x小时追上甲,那么根据王丽x小时走的路程和张强(x+4)路程相等即可列出方程,解此方程即可.
解答 解:设王丽x小时追上张强,
依题意得($\frac{1}{5}$-$\frac{1}{11}$)x=4×$\frac{1}{11}$,
解得x=$\frac{20}{6}$.
上午10时+$\frac{20}{6}$小时=下午1点20分.
故王丽下午1点20分追上张强的.
点评 考查了一元一次方程的应用,此题解题思想比较新颖,把行程问题当做工程问题去解决.在很多行程问题中有时无法利用行程问题的思想直接解决就采用这种方法,注意使用这种方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
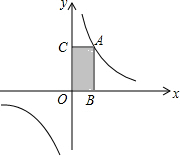 如图,反比例函数y=$\frac{k}{x}$的图象过点A,过点A分别向x轴和y轴作垂线,垂足为B和C.若矩形ABOC的面积为2,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$的图象过点A,过点A分别向x轴和y轴作垂线,垂足为B和C.若矩形ABOC的面积为2,则k的值为( )| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
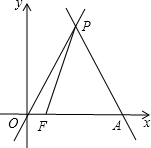 已知:如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴相交于点A,与直线y=$\sqrt{3}$x交于点P.
已知:如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴相交于点A,与直线y=$\sqrt{3}$x交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形 | B. | 对角线互相平分的四边形 | ||
| C. | 对角线互相垂直且相等的四边形 | D. | 对角线互相垂直的四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com