
【题目】图1是一个长为2m,宽为2n的长方形,将该长方形沿图中虚线用剪刀均分成四块小长方形,然后按照图2所示拼成一个正方形.
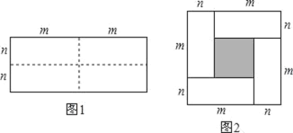
(1)使用不同方法计算图2中小正方形的面积,可推出(m+n)2,(m-n)2,mn之间的等量关系为: ;
(2)利用(1)中的结论,解决下列问题:
①已知a-b=4,ab=5,求a+b的值;
②已知a>0,a-![]() =2,求a+
=2,求a+![]() 的值.
的值.
【答案】(1)(m-n)2=(m+n)2-4mn;(2)①6或-6;②4.
【解析】
(1)由题意知,阴影部分小正方形的边长为m-n.根据正方形的面积公式即可求出图中阴影部分的面积,也可以用大正方形的面积减去四个小长方形的面积求图中阴影部分的面积,
利用两种求法确定出所求关系式即可;
(2)①利用(1)的结论,可知(a-b)2=(a+b)2-4ab,把已知数值整体代入即可;②先利用完全平方公式进行变形,即将a-![]() =2两边同时平方,然后求出(a+
=2两边同时平方,然后求出(a+![]() )2的值,从而得出结果.
)2的值,从而得出结果.
解:(1)阴影部分的面积可以看作是边长m-n的正方形的面积,也可以看作边长m+n的正方形的面积减去4个小长方形的面积,
∴(m-n)2=(m+n)2-4mn,
故答案为:(m-n)2=(m+n)2-4mn;
(2)①∵a-b=4,ab=5,且由(1)知(a-b)2=(a+b)2-4ab,
∴(a+b)2=16+20=36,
∴a+b=6或-6;
②∵a-![]() =2,
=2,
∴(a-![]() )2= a2-6+
)2= a2-6+![]() =4,
=4,
∴a2+6+![]() =16,
=16,
∴(a+![]() )2=16,
)2=16,
又a>0,∴a+![]() =4.
=4.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
(Ⅰ)求△ABC的面积;
(Ⅱ)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
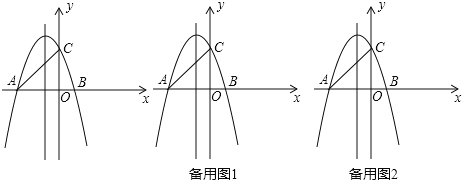
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,因此 4,12,20 都是“神秘数”,则下面哪个数是“神秘数”( )
A.56B.60C.62D.88
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A. 255054 B. 255064 C. 250554 D. 255024
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
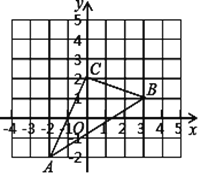
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王先生到市行政中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作-1,王先生从1楼出发,电梯上下楼层依次记录如下(单位:层):![]() .
.
(1)请你通过计算说明王先生最后是否回到出发点![]() 楼.
楼.
(2)该中心大楼每层高3m,电梯每向上或下1m需要耗电0.3度,根据王先生现在所处位置,请你算算,他办事时电梯需要耗电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com