
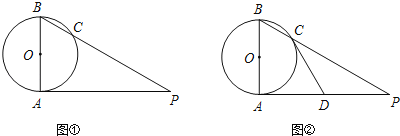
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若直线CD是⊙O的切线,求证:D为AP的中点.
【答案】(1)55°(2)见解析
【解析】
(1)易证PA⊥AB,再通过解直角三角形求解;
(2)连接OC、AC,证出OC⊥CD,AB⊥AP,根据半径所对应的角相等即可证明CD= AD;根据AB是O的直径,得出∠BCA=90°,再根据两个角相加为90°,即可证明CD= DP,从而得出结论
(1)∵AB是⊙O的直径,AP是⊙O的切线
∴PA⊥AB
∴∠BAP=90°
∵∠P=35°
∴∠ABP=∠BAP-∠P=90°-35°=55°
故答案为:55°
(2)如图,连接OC、AC
∵CD是⊙O的切线
∴OC⊥CD
∴∠1+∠3=90°
∵AP是⊙O的切线
∴AB⊥AP
∴∠2+∠4=90°
∵OA= OC
∴∠1=∠2
∴∠3=∠4
∴ CD= AD
∵AB是O的直径,
∴∠BCA=90°
∴∠DCP+∠3=90°
∠CPA+∠4=90°
∴∠DCP=∠CPA
∴CD= DP
∴CD= DP=AD
∴D为AP的中点


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于两点A,B,给出如下定义:以线段AB为边的正方形称为点A,B的“确定正方形”.如图为点A,B 的“确定正方形”的示意图.
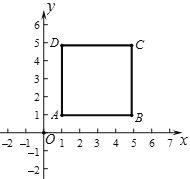
(1)如果点M的坐标为(0,1),点N的坐标为(3,1),那么点M,N的“确定正方形”的面积为___________;
(2)已知点O的坐标为(0,0),点C为直线![]() 上一动点,当点O,C的“确定正方形”的面积最小,且最小面积为2时,求b的值.
上一动点,当点O,C的“确定正方形”的面积最小,且最小面积为2时,求b的值.
(3)已知点E在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为P(m,0),点F在直线![]() 上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围.
上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种泰山旅游纪念品,4月份的营业额为2000元,为扩大销售量,5月份该商店对这种纪念品打9折销售,结果销售量增加20件,营业额增加700元.
(1)求该种纪念品4月份的销售价格;
(2)若4月份销售这种纪念品获利800元,5月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了准备“欢乐颂——创意市场”,初2020级某同学到批发市场购买了![]() 、
、![]() 两种原材料,
两种原材料,![]() 的单价为每件6元,
的单价为每件6元,![]() 的单价为每件3元.该同学的创意作品需要
的单价为每件3元.该同学的创意作品需要![]() 材料的数量是
材料的数量是![]() 材料数量的2倍,同时,为了减少成本,该同学购买原材料的总费用不超过480元.
材料数量的2倍,同时,为了减少成本,该同学购买原材料的总费用不超过480元.
(1)该同学最多购买多少件![]() 材料;
材料;
(2)在该同学购买![]() 材料最多的前提下,用所购买的
材料最多的前提下,用所购买的![]() ,
,![]() 两种材料全部制作作品,在制作中其他费用共花了520元,活动当天,该同学在成本价(购买材料费用+其他费用)的基础上整体提高
两种材料全部制作作品,在制作中其他费用共花了520元,活动当天,该同学在成本价(购买材料费用+其他费用)的基础上整体提高![]() 标价,但无人问津,于是该同学在标价的基础上降低
标价,但无人问津,于是该同学在标价的基础上降低![]() 出售,最终,在活动结束时作品卖完,这样,该同学在本次活动中赚了
出售,最终,在活动结束时作品卖完,这样,该同学在本次活动中赚了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图1、图2分别是![]() 的网格,网格中的每个小正方形的边长均为1.请按下列要求分别画出相应的图形,且所画图形的每个顶点均在所给小正方形的顶点上.
的网格,网格中的每个小正方形的边长均为1.请按下列要求分别画出相应的图形,且所画图形的每个顶点均在所给小正方形的顶点上.

(1)在图1中画出一个周长为![]() 的菱形
的菱形![]() (非正方形);
(非正方形);
(2)在图2中画出一个面积为9的平行四边形![]() ,且满足
,且满足![]() ,请直接写出平行四边形
,请直接写出平行四边形![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com