
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )


A.S=AD•CE B.S>AD•CE C.S<AD•CE D.无法确定
A【考点】勾股定理;三角形的面积.
【专题】计算题.
【分析】根据△BCD与△ACD的周长相等,我们可得出:BC+BD=AC+AD,等式的左右边正好是三角形ABC周长的一半,即
 ,有BC,AC的值,那么就能求出BD的长了,同理可求出AE的长;表示出AE•BD,即可找出与S的大小关系.
,有BC,AC的值,那么就能求出BD的长了,同理可求出AE的长;表示出AE•BD,即可找出与S的大小关系.
【解答】解:∵△BCD与△ACD的周长相等,BC=a,AC=b,AB=c,
∴BC+BD=AC+AD=
 ,
,
∴AD=
 ﹣b=
﹣b=
 ,
,
同理CE=
 ,
,
∵∠BCA=90°,
∴a2+b2=c2,S=
 ab,
ab,
可得CE•AD=
 ×
×
 =
=
 =
=
 (c2﹣a2﹣b2+2ab)=
(c2﹣a2﹣b2+2ab)=
 ab,
ab,
则S=CE•AD.
故选A.
【点评】此题考查了勾股定理,以及三角形面积,通过周长相等得出线段的长是解题的关键.


科目:初中数学 来源: 题型:
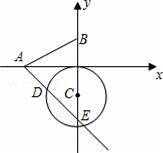
如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )

A.3 B.
 C.
C.
 D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一个三角形的第一条边长为2a+5b,第二条边比第一条边长3a﹣2b,第三条边比第二条边短3a
(1)用含a,b的式子表示这个三角形的周长,并化简;
(2)若a,b满足|a﹣5|+(b﹣3)2=0,求出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读材料:
我们知道,4x+2x﹣x=(4+2﹣1)x=5x,类似地,我们把(a+b)看成一个整体,则4(a+b)+2(a+b)﹣(a+b)﹣(4+2﹣1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a﹣b)看成一个整体,合并3(a﹣b)2﹣7(a﹣b)2+2(a﹣b)2的结果是C.
A.﹣6(a﹣b)2 B.6(a﹣b)2 C.﹣2(a﹣b)2 D.2(a﹣b)2
(2)已知x2+2y=5,求3x2+6y﹣21的值;
拓广探索:
(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
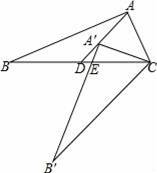
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com