
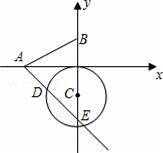
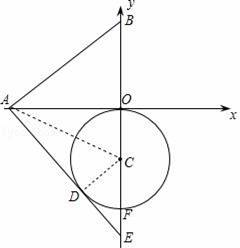
如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )

A.3 B.
 C.
C.
 D.4
D.4
B【考点】切线的性质;三角形的面积.
【专题】计算题;压轴题.
【分析】当射线AD与⊙C相切时,△ABE面积的最大.设EF=x,由切割线定理表示出DE,可证明△CDE∽△AOE,根据相似三角形的性质可求得x,然后求得△ABE面积.
【解答】解:当射线AD与⊙C相切时,△ABE面积的最大.
连接AC,
∵∠AOC=∠ADC=90°,AC=AC,OC=CD,
∴Rt△AOC≌Rt△ADC,
∴AD=AO=2,
连接CD,设EF=x,
∴DE2=EF•OE,
∵CF=1,
∴DE=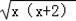
 ,
,
∴△CDE∽△AOE,
∴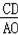
 =
=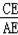
 ,
,
即
 =
=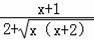
 ,
,
解得x=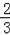
 ,
,
S△ABE=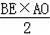
 =
=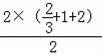
 =
=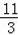
 .
.
故选:B.

【点评】本题是一个动点问题,考查了切线的性质和三角形面积的计算,解题的关键是确定当射线AD与⊙C相切时,△ABE面积的最大.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
李勇购买80分与100分的邮票共16枚,花了14元6角,购买80分与100分的邮票的枚数分别是( )
A、6,10 B、7,9 C、8,8 D、9,7
查看答案和解析>>
科目:初中数学 来源: 题型:
工作人员检验4个零件的长度,超过标准长度的记作正数,不足标准长度的记作负数(单位:mm),从长度的角度看,下列记录的数据中最接近标准长度的是( )
A.﹣3 B.﹣1 C.2 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )


A.S=AD•CE B.S>AD•CE C.S<AD•CE D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题是真命题的有( )
①对顶角相等;
②两直线平行,内错角相等;
③两个锐角对应相等的两个直角三角形全等;
④有三个角是直角的四边形是矩形;
⑤平分弦的直径垂直于弦,并且平分弦所对的弧.
A..1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一次函数的图象经过点P(3,5),且平行于直线y=2x.
(1)求该一次函数的解析式;
(2)若点Q(x,y)在该直线上,且在x轴的下方,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com