
已知一次函数的图象经过点P(3,5),且平行于直线y=2x.
(1)求该一次函数的解析式;
(2)若点Q(x,y)在该直线上,且在x轴的下方,求x的取值范围.
【考点】待定系数法求一次函数解析式;一次函数图象上点的坐标特征.
【分析】(1)根据两直线平行可知该一次函数斜率k=2,设出解析式,将点P坐标代入可得;
(2)根据直线上的点Q在x轴下方可得y<0,解不等式可得x的范围.
【解答】解:(1)∵一次函数的图象平行于直线y=2x,可设该一次函数解析式为y=2x+b,
∴将点P(3,5)代入得:6+b=5,
解得:b=﹣1,
故一次函数解析式为:y=2x﹣1;
(2)∵点Q(x,y)在x轴下方,
∴y=2x﹣1<0,
解得:x<
 .
.
【点评】本题主要考查一次函数解析式及图象上的点的坐标,待定系数法求出解析式是前提,根据点的位置确定函数值小于0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
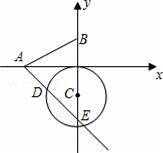
如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )

A.3 B.
 C.
C.
 D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
为了防控流感,某校积极进行校园环境消毒,购买了甲、乙两种消毒液共100瓶。其中甲种6元/瓶,乙种9元/瓶。
(1)如果购买这两种消毒液共用780元。求甲乙两种消毒液各购买多少瓶?
(2)该校准备再次购买这两种消毒液(不包括已经购买的100瓶),使乙种瓶数是甲种瓶数的2倍,且所需费用不超过1200元(不包括780元),则甲种消毒液最多能再买多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
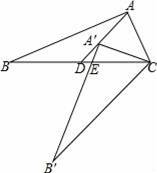
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com