
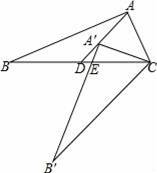
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE= .

4:3 .
【考点】旋转的性质;三角形的重心.
【专题】计算题;平移、旋转与对称.
【分析】先证明DA′=
 CB′,由DA′∥CB′,得
CB′,由DA′∥CB′,得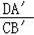
 =
=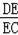
 =
=
 即可解决问题.
即可解决问题.
【解答】证明:∵∠BAC=90°,A′是△ABC重心,
∴BD=DC=AD,DA′=
 AA′=
AA′=
 AD=
AD=
 BC,
BC,
∵△A′CB′S是由△ABC旋转得到,
∴CA′=CA,BC=CB′,∠ACB=∠A′CB′=∠DAC,∠CA′B′=90°,
∴∠CAA′=∠CA′A=∠DAC,∠DA′B′+′CA′A=90°,∠B′+∠A′CB′=90°,
∴∠DA′B′=∠B′
∴DA′∥CB′,
∴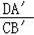
 =
=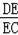
 =
=
 ,设DE=k,则EC=6k,BE=DC=7k,BE=8k,
,设DE=k,则EC=6k,BE=DC=7k,BE=8k,
∴BE:CE=8k:6k=4:3.
故答案为4:3.
【点评】本题考查三角形重心、旋转平行线分线段成比例定理等知识,解题的关键是发现DA′=
 CB′,记住三角形的重心把中线分成1:2两部分,属于中考常考题型.
CB′,记住三角形的重心把中线分成1:2两部分,属于中考常考题型.


科目:初中数学 来源: 题型:
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )


A.S=AD•CE B.S>AD•CE C.S<AD•CE D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐10元的人数占年级总人数的25%,则本次捐款20元的人数为 人.


查看答案和解析>>
科目:初中数学 来源: 题型:
已知一次函数的图象经过点P(3,5),且平行于直线y=2x.
(1)求该一次函数的解析式;
(2)若点Q(x,y)在该直线上,且在x轴的下方,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com