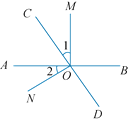
[题目]如图.直线AB.CD相交于点O.过点O作两条射线OM.ON.且∠AOM＝∠CON＝90°.(1)若OC平分∠AOM.求∠AOD的度数,(2)若∠1＝∠BOC.求∠AOC和∠MOD. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，直线AB，CD相交于点O，过点O作两条射线OM，ON，且∠AOM＝∠CON＝90°.

(1)若OC平分∠AOM，求∠AOD的度数；

(2)若∠1＝∠BOC，求∠AOC和∠MOD.

【答案】（1）135°（2）150°

【解析】

①根据角平分线定义求出∠1=∠AOC=45°，代入∠AOD=180°-∠AOC求出即可；
②求出∠BOM=180°-90°=90°，根据∠1=∠BOC求出∠1=∠BOM=30°，即可求出答案．

(1)因为∠AOM＝∠CON＝90°，OC平分∠AOM，所以∠1＝∠AOC＝45°，所以∠AOD＝180°－∠AOC＝180°－45°＝135°.

(2)因为∠AOM＝90°，所以∠BOM＝180°－90°＝90°.因为∠1＝∠BOC，所以∠1＝∠BOM＝30°，所以∠AOC＝90°－30°＝60°，∠MOD＝180°－30°＝150°.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】解方程组：(1) ;

(2) ;

(3) ;

(4) .

查看答案和解析>>

科目：初中数学 来源： 题型：

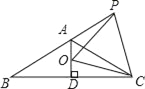
【题目】如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC．

（1）求∠APO+∠DCO的度数；

（2）求证：点P在OC的垂直平分线上．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABC经过一次平移到△DFE的位置，请回答下列问题：

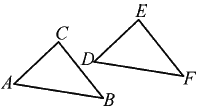
(1)点C的对应点是点__________，∠D=__________，BC=__________；

(2)连接CE，那么平移的方向就是__________的方向，平移的距离就是线段__________的长度；

(3)连接AD，BF，BE，与线段CE相等的线段有__________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】深圳市某学校抽样调查，A类学生骑共享单车，B类学生坐公交车、私家车等，C类学生步行，D类学生（其它），根据调查结果绘制了不完整的统计图．

类型	频数	频率
A	30
B	18	0.15
C		0.40
D

（1）学生共人，，；
（2）补全条形统计图；
（3）若该校共有2000人，骑共享单车的有人．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了锻炼学生身体素质，训练定向越野技能，某校在一公园内举行定向越野挑战赛．路线图如图1所示，点E为矩形ABCD边AD的中点，在矩形ABCD的四个顶点处都有定位仪，可监测运动员的越野进程，其中一位运动员P从点B出发，沿着B﹣E﹣D的路线匀速行进，到达点D．设运动员P的运动时间为t，到监测点的距离为y．现有y与t的函数关系的图象大致如图2所示，则这一信息的来源监测点为（）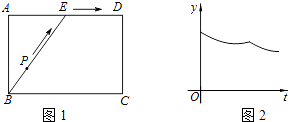

A.A点
B.B点
C.C点
D.D点