
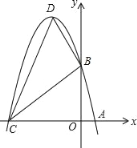
【题目】已知:m,n是方程x2﹣6x+5=0的两个实数根,且m<n,抛物线y=﹣x2+bx+c的图象经过点A(m,0),B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标和△BCD的面积.
【答案】(1)y=﹣x2﹣4x+5;(2)15.
【解析】
(1)首先解方程求得m和n的值,得到A和B的坐标,然后利用待定系数法即可求得解析式;
(2)首先求得C和D的坐标,作DE⊥y轴于点E,根据S△BCD=S梯形OCDE﹣S△DEB﹣S△OBC求解.
解:(1)解方程x2﹣6x+5=0,
解得:x1=1,x2=5,
则m=1,n=5.
A的坐标是(1,0),B的坐标是(0,5).
代入二次函数解析式得:![]() ,
,
解得:![]() ,
,
则函数的解析式是y=﹣x2﹣4x+5;
(2)解方程﹣x2﹣4x+5=0,
解得:x1=﹣5,x2=1.
则C的坐标是(﹣5,0).
y=﹣x2﹣4x+5=﹣(x2+4x+4)+9=﹣(x+2)2+9
则D的坐标是(﹣2,9).
作DE⊥y轴于点E,则E坐标是(0,9).
则S梯形OCDE=![]() (OC+DE)OE=
(OC+DE)OE=![]() ×(2+5)×9=
×(2+5)×9=![]() ,
,
S△DEB=![]() BEDE=
BEDE=![]() ×4×2=4,
×4×2=4,
S△OBC=![]() OCOB=
OCOB=![]() ×5×5=
×5×5=![]() ,
,
则S△BCD=S梯形OCDE﹣S△DEB﹣S△OBC=![]() ﹣4﹣
﹣4﹣![]() =15.
=15.


科目:初中数学 来源: 题型:
【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表8.
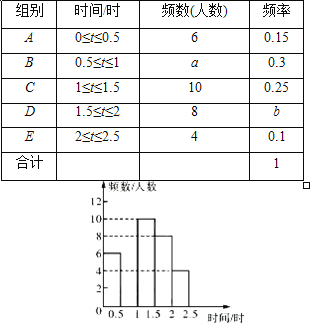
请根据图表中的信息,解答下列问题:
(1)表中的a=______,b=______,中位数落在________组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作读书心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
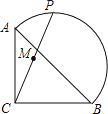
【题目】如图,在等腰RtABC中,![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
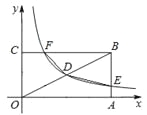
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数![]() (
(![]() )在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则
)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com