
【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).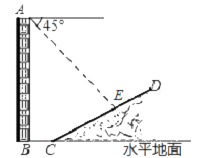
【答案】解:过点E作EF⊥BC于点F,EH⊥AB于点H.
∴∠EFC=∠EHA=∠EHB=∠HBC=90°.
∴四边形HBFE是矩形,
∴HE=BF,HB=EF,
∵在Rt△CEF中,CE=20,∠ECF=30°
∴EF= ![]() CE=10,CF=CE
CE=10,CF=CE ![]() cos30°=
cos30°= ![]() ,
,
∴HB=EF=10,BF=BC+CF= ![]() ,
,
∴HE=BF= ![]() ,
,
∵在Rt△AHE中,∠HAE=90°-45°=45°,
∴AH=HE= ![]() ,
,
∴AB=AH+BH=10+10 ![]() +10=20+10
+10=20+10 ![]() (米)
(米)
答:楼房AB的高为(20+10 ![]() )米.
)米.
【解析】根据已知条件山坡斜面CD与水平面夹角为30°,CE=20米,因此过点E作EF⊥BC于点F,利用解直角三角形求出CF、EF的长,由BC=10米得出BF的长,再根据已知条件小丽从楼房顶测得点E的俯角为45°,因此过点E作EH⊥AB于点H.易证得四边形HBFE是矩形,得出HE的长。从而得到AH的长,然后根据AB=AH+BH,即可求得结果。


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
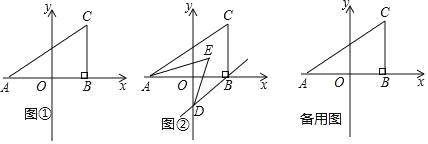
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
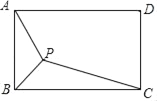
【题目】如图,矩形ABCD中,AB=2![]() ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
A. 4![]() +3B. 2
+3B. 2![]() C. 2
C. 2![]() +6D. 4
+6D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com