
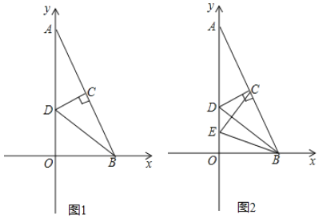
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 轴与点
轴与点![]() ,连接
,连接![]() ,
,![]() 为第一象限内的点.
为第一象限内的点.
(1)求点![]() 坐标;
坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)如图2,点![]() 为
为![]() 轴上的一个动点,当
轴上的一个动点,当![]() 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)a=6;(3)
;(2)a=6;(3) ![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)设OD=x,则AD=8-x,由线段垂直平分线的性质得BD=AD=8-x,在Rt△BOD中,由勾股定理得出方程,解方程即可得出D点坐标;
(2)设直线BD的解析式为y=kx+b,由待定系数法即可得出解析式,由题意得出△DBC与△DBM是同底等高的三角形,得出BD与直线CM平行,求出直线CM的解析式为![]() ;把M(a,1)代入
;把M(a,1)代入![]() ,求出a=6即可;
,求出a=6即可;
(3)由勾股定理求出AB,得出![]() ,由勾股定理求出
,由勾股定理求出![]() ,分三种情况:①EC=ED时,②DC=DE时;③CE=CD时;分别求出点E的坐标即可.
,分三种情况:①EC=ED时,②DC=DE时;③CE=CD时;分别求出点E的坐标即可.
解:(1)∵B(4,0),A(0,8)
∴OA=8,OB=4
设OD=x,则AD=8-x
∵AB的垂直平分线交与y轴于点D
∴BD=AD=8-x
在Rt△BOD中,由勾股定理得:![]()
![]()
∴x=3
∴D(0,3)
(2)设直线BD的解析式为y=kx+b,
把B(4,0)和D(0,3)代入y=kx+b得:
![]()
∴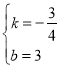
则直线BD的解析式为![]()
∵![]() 时,
时,
∴△DBC与△DBM同是底为BD,且高相等的三角形
∴直线BD与直线CM平行
设CM的解析式为![]() ,
,
∵CD是AB的垂直平分线
∴C是AB的中点
∵B(4,0),A(0,8),
∴C(2,4)
把C(2,4)代入![]() 得:
得:![]() ,
,
解得:![]()
∴直线CM的解析式为![]()
又因为M(a,1)且在第一象限
∴![]()
解得:a=6
(3)由勾股定理得,![]()
∵点C为边AB的中点
∴![]()
∵AD=OA-OD=5
∴![]()
设E(0,x),则![]()
分三种情况:①EC=ED时, 过E作EQ⊥CD于Q,如图所示:
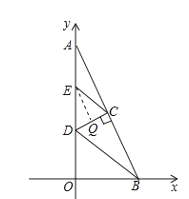
则EQ∥AB
∴Q为CD的中点
∴E为AD的中点
∴AE=ED
∴8-x=x-3
解得:![]()
![]()
②DC=DE时
∴![]()
∴![]() 或
或![]()
∴![]() 或
或![]()
③CE=CD时,过C作CF⊥AO交于F,如图所示:
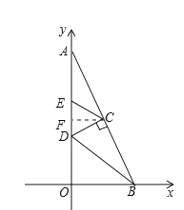
∴∠AFC=∠AOB=90°F为ED中点
∴FC//OB,EF=DF
∵C为AB的中点
∴F为AO的中点,
∵A(0,8),O(0,0)
∴F(0,4)
∴EF=DF=1
∴x-4=1
∴x=5
∴E(0,5)
综上所述:当△CDE为等腰三角形时,E点的坐标为![]() 或
或![]() 或
或![]() 或
或![]()


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )

A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省济宁市)如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )

A. 60B. 80C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
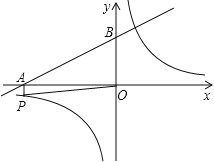
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,CD、C′D′表示小明所在两个不同位置:
(1)分别画出这两个不同位置小明的影子;
(2)小明发现在这两个不同的位置上,他的影子长分别是自己身高的1倍和2倍,他又量得自己的身高为1.5米,DD′长为3米,你能帮他算出路灯的高度吗?(B、D、D′在一条直线上)
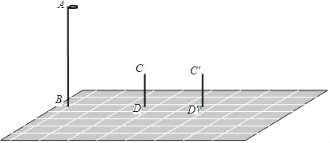
查看答案和解析>>
科目:初中数学 来源: 题型:
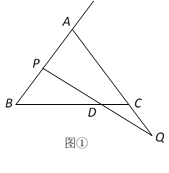
【题目】已知△ABC中,AB=AC,点P是AB上一动点,点Q是AC的延长线上一动点,且点P从B运动向A、点Q从C运动向Q移动的时间和速度相同,PQ与BC相交于点D,若AB=![]() ,BC=16.
,BC=16.
(1)如图1,当点P为AB的中点时,求CD的长;
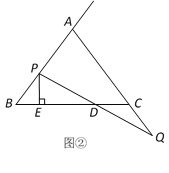
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,设BE+CD=λ,λ是否为常数?若是请求出λ的值,若不是请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快200m,两人同时从起点同向出发,经过3min两人首次相遇,此时乙还需跑150m才能跑完第一圈.
![]() 求甲、乙两人的速度分别是每分钟多少米?
求甲、乙两人的速度分别是每分钟多少米?![]() 列方程或者方程组解答
列方程或者方程组解答![]()
![]() 若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过
若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过![]() 两人再次相遇,则乙的速度至少要提高每分钟多少米?
两人再次相遇,则乙的速度至少要提高每分钟多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
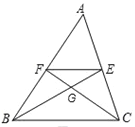
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com