
ΓΨΧβΡΩΓΩΆ§―ßΟ«Θ§‘Ύ≥θ“Μ―ßœΑ’ΐΕύ±Ώ–ΈΚΆ‘≤’βΫΎΩΈ ±Θ§Έ“Ο«ΨΆ―ßœΑΙΐΥΡ±Ώ–ΈΒΡΡΎΫ«ΚΆΒ»”Ύ360ΓψΘ°œ¬ΟφΈ“Ο«ΨΆ‘ΎΥΡ±Ώ–Έ÷–ά¥―–ΨΩΦΗΗωΈ ΧβΘΚ
(1)Έ Χβ±≥ΨΑΘΚ
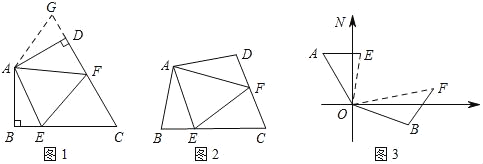
»γΆΦ1ΘΚ‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ABΘΫADΘ§ΓœBADΘΫ120ΓψΘ§ΓœBΘΫΓœADCΘΫ90ΓψΘ§EΓΔFΖ÷±π «BCΓΔCD…œΒΡΒψΘ§«“ΓœEAFΘΫ60ΓψΘ§ΧΫΨΩΆΦ÷–œΏΕΈBEΓΔEFΓΔFD÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
–ΓΆθΆ§―ßΧΫΨΩ¥ΥΈ ΧβΒΡΖΫΖ® «Θ§―”≥ΛFDΒΫΒψGΘ§ ΙDGΘΫBEΘ°Ν§ΫαAGΘ§œ»÷ΛΟςΓςABEΓ’ΓςADGΘ§‘Ό÷ΛΟςΓςAEFΓ’ΓςAGFΘ§Ω…ΒΟ≥ωΫα¬έΘ§ΥϊΒΡΫα¬έ”Π «______ΘΜ
(2)ΧΫΥς―”…λΘΚ
»γΆΦ2Θ§»τ‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ABΘΫADΘ§ΓœB+ΓœDΘΫ180ΓψΘ§EΓΔFΖ÷±π «BCΓΔCD…œΒΡΒψΘ§«“ΓœEAFΘΫ![]() ΓœBADΘ§…œ ωΫα¬έ «Ζώ»‘≥…ΝΔΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΓœBADΘ§…œ ωΫα¬έ «Ζώ»‘≥…ΝΔΘ§≤ΔΥΒΟςάμ”…ΘΜ
(3) ΒΦ ”Π”ΟΘΚ
»γΆΦ3Θ§‘ΎΡ≥¥ΈΨϋ ¬―ίœΑ÷–Θ§ΫΔΆßΦΉ‘Ύ÷ΗΜ”÷––Ρ(ΒψO¥Π)±±ΤΪΈς30ΓψΒΡA¥ΠΘ§ΫΔΆß““‘Ύ÷ΗΜ”÷––ΡΡœΤΪΕΪ70ΓψΒΡB¥ΠΘ§≤Δ«“ΝΫΫΔΆßΒΫ÷ΗΜ”÷––ΡΒΡΨύάκœύΒ»Θ°Ϋ”ΒΫ––Ε·÷ΗΝνΚσΘ§ΫΔΆßΦΉœρ’ΐΕΪΖΫœρ“‘45ΚΘάο/ ±ΒΡΥΌΕ»«ΑΫχΘ§Ά§ ±Θ§ΫΔΆß““―Ί±±ΤΪΈς50ΓψΒΡΖΫœρ“‘60ΚΘάο/ ±ΒΡΥΌΕ»«ΑΫχΘ§2–Γ ±ΚσΘ§÷ΗΜ”÷––ΡΙέ≤λΒΫΦΉΓΔ““ΝΫΫΔΆßΖ÷±πΒΫ¥οEΓΔF¥ΠΘ§«“ΝΫΫΔΆß÷°ΦδΒΡΦ–Ϋ«ΈΣ70ΓψΘ§ ‘«σ¥Υ ±ΝΫΫΔΆß÷°ΦδΒΡΨύάκΘ°
ΓΨ¥πΑΗΓΩ(1)EFΘΫBE+DFΘΜ(2)Ϋα¬έEFΘΫBE+DF»‘»Μ≥…ΝΔΘΜ(3)¥Υ ±ΝΫΫΔΆß÷°ΦδΒΡΨύάκ «210ΚΘάοΘ°
ΓΨΫβΈωΓΩ
(1)―”≥ΛFDΒΫΒψG. ΙDG=BE.Ν§ΫαAG,Φ¥Ω…÷ΛΟςΓςABEΓ’ΓςADG,Ω…ΒΟAE=AG,‘Ό÷ΛΟςΓςAEFΓ’ΓςAGF,Ω…ΒΟEF=FG,Φ¥Ω…ΫβΧβ;
(2)―”≥ΛFDΒΫΒψG. ΙDG=BE.Ν§ΫαAG,Φ¥Ω…÷ΛΟςΓςABEΓ’ΓςADG,Ω…ΒΟAE=AG,‘Ό÷ΛΟςΓςAEFΓ’ΓςAGF,Ω…ΒΟEF=FG,Φ¥Ω…ΫβΧβ
(3)Ν§Ϋ”EF,―”≥ΛAEΓΔBFœύΫΜ”ΎΒψC,»ΜΚσ”κ(2)Ά§άμΩ…÷Λ.
ΫβΘΚ(1)EFΘΫBE+DFΘ§÷ΛΟς»γœ¬ΘΚ
‘ΎΓςABEΚΆΓςADG÷–Θ§
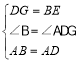 Θ§
Θ§
ΓύΓςABEΓ’ΓςADG(SAS)Θ§
ΓύAEΘΫAGΘ§ΓœBAEΘΫΓœDAGΘ§
ΓΏΓœEAFΘΫ![]() ΓœBADΘ§
ΓœBADΘ§
ΓύΓœGAFΘΫΓœDAG+ΓœDAFΘΫΓœBAE+ΓœDAFΘΫΓœBAD©¹ΓœEAFΘΫΓœEAFΘ§
ΓύΓœEAFΘΫΓœGAFΘ§
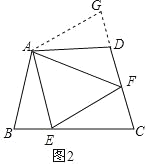
‘ΎΓςAEFΚΆΓςGAF÷–Θ§
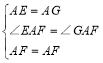 Θ§
Θ§
ΓύΓςAEFΓ’ΓςAGF(SAS)Θ§
ΓύEFΘΫFGΘ§
ΓΏFGΘΫDG+DFΘΫBE+DFΘ§
ΓύEFΘΫBE+DFΘΜ
Ι ¥πΑΗΈΣ EFΘΫBE+DFΘ°
(2)Ϋα¬έEFΘΫBE+DF»‘»Μ≥…ΝΔΘΜ
άμ”…ΘΚ―”≥ΛFDΒΫΒψGΘ° ΙDGΘΫBEΘ°Ν§ΫαAGΘ§»γΆΦ2Θ§
‘ΎΓςABEΚΆΓςADG÷–Θ§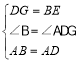 Θ§
Θ§
ΓύΓςABEΓ’ΓςADG(SAS)Θ§
ΓύAEΘΫAGΘ§ΓœBAEΘΫΓœDAGΘ§
ΓΏΓœEAFΘΫ![]() ΓœBADΘ§
ΓœBADΘ§
ΓύΓœGAFΘΫΓœDAG+ΓœDAFΘΫΓœBAE+ΓœDAFΘΫΓœBAD©¹ΓœEAFΘΫΓœEAFΘ§
ΓύΓœEAFΘΫΓœGAFΘ§
‘ΎΓςAEFΚΆΓςGAF÷–Θ§
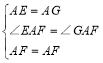 Θ§
Θ§
ΓύΓςAEFΓ’ΓςAGF(SAS)Θ§
ΓύEFΘΫFGΘ§
ΓΏFGΘΫDG+DFΘΫBE+DFΘ§
ΓύEFΘΫBE+DFΘΜ
(3)»γΆΦ3Θ§Ν§Ϋ”EFΘ§―”≥ΛAEΓΔBFœύΫΜ”ΎΒψCΘ§
ΓΏΓœAOBΘΫ30Γψ+90Γψ+(90Γψ©¹70Γψ)ΘΫ140ΓψΘ§ΓœEOFΘΫ70ΓψΘ§
ΓύΓœEOFΘΫ![]() ΓœAOBΘ§
ΓœAOBΘ§
”÷ΓΏOAΘΫOBΘ§ΓœOAC+ΓœOBCΘΫ(90Γψ©¹30Γψ)+(70Γψ+50Γψ)ΘΫ180ΓψΘ§
ΓύΖϊΚœΧΫΥς―”…λ÷–ΒΡΧθΦΰΘ§
ΓύΫα¬έEFΘΫAE+BF≥…ΝΔΘ§
Φ¥EFΘΫ2ΓΝ(45+60)ΘΫ210(ΚΘάο)Θ°
¥πΘΚ¥Υ ±ΝΫΫΔΆß÷°ΦδΒΡΨύάκ «210ΚΘάοΘ°


 ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
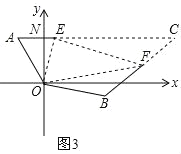
ΓΨΧβΡΩΓΩΓςABC÷–Θ§AB=AC.
Θ®1Θ©»γΆΦ1Θ§»γΙϊΓœBAD=30ΓψΘ§AD «BC…œΒΡΗΏΘ§AD=AEΘ§‘ρΓœEDC=_____Ε»ΘΜ
Θ®2Θ©»γΆΦ2Θ§»γΙϊΓœBAD=40ΓψΘ§AD «BC…œΒΡΗΏΘ§AD=AEΘ§‘ρΓœEDC=_______Ε»ΘΜ
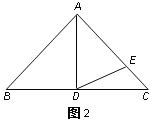
Θ®3Θ©ΥΦΩΦΘΚΆ®Ιΐ“‘…œΝΫΧβΘ§ΡψΖΔœ÷ΓœBAD”κΓœEDC÷°Φδ”– ≤Ο¥ΙΊœΒΘΩ«κ”Ο ΫΉ”±μ ΨΘΚ____________________.
Θ®4Θ©»γΆΦ3Θ§»γΙϊAD≤Μ «BC…œΒΡΗΏΘ§AD=AEΘ§ «Ζώ»‘”–…œ ωΙΊœΒΘΩ»γ”–Θ§«κΡψ–¥≥ωά¥Θ§≤ΔΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ζ¥±»άΐΚ· ΐ y=![]() ΒΡΆΦœσ”κ“Μ¥ΈΚ· ΐyΘΫmxΘΪbΒΡΆΦœσΫΜ”ΎΝΫΒψAΘ®1,3Θ©,BΘ®n,Θ≠1Θ©Θ°
ΒΡΆΦœσ”κ“Μ¥ΈΚ· ΐyΘΫmxΘΪbΒΡΆΦœσΫΜ”ΎΝΫΒψAΘ®1,3Θ©,BΘ®n,Θ≠1Θ©Θ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐ”κ“Μ¥ΈΚ· ΐΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©ΗυΨίΆΦœσΘ§ΜΊ¥πΒ±“Μ¥ΈΚ· ΐΒΡ÷Β¥σ”ΎΖ¥±»άΐΚ· ΐΒΡ÷Β ±Θ§x ΒΡ»Γ÷ΒΖΕΈßΈΣ________ΘΜ
(3) Ν§Ϋ”AOΓΔBOΘ§‘ρΓςABOΒΡΟφΜΐ «_________ΘΜ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΆ§“ΜΉχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐy=©¹mx+n2”κΕΰ¥ΈΚ· ΐy=x2+mΒΡΆΦœσΩ…Ρή «Θ®ΓΓΓΓΘ©
A. 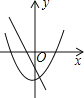 B.
B. 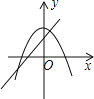 C.
C. 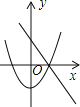 D.
D. 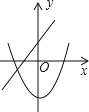
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§Ε‘Ϋ«œΏACΓΔBDœύΫΜ”ΎΒψGΘ§EΓΔFΖ÷±π «±ΏADΓΔBCΒΡ÷–ΒψΘ§ABΘΫ2Θ§BCΘΫ4Θ§“ΜΕ·ΒψP¥”ΒψB≥ωΖΔΘ§―ΊΉ≈B©¹A©¹D©¹CΒΡΖΫœρ‘ΎΨΊ–ΈΒΡ±Ώ…œ‘ΥΕ·Θ§‘ΥΕ·ΒΫΒψCΆΘ÷ΙΘ°ΒψMΈΣΆΦ1÷–ΒΡΡ≥ΗωΕ®ΒψΘ§…ηΒψP‘ΥΕ·ΒΡ¬Ζ≥ΧΈΣxΘ§ΓςBPMΒΡΟφΜΐΈΣyΘ§±μ Ψy”κxΒΡΚ· ΐΙΊœΒΒΡΆΦœσ¥σ÷¬»γΆΦ2Υυ ΨΘ°Ρ«Ο¥Θ§ΒψMΒΡΈΜ÷ΟΩ…Ρή «ΆΦ1÷–ΒΡΘ®ΓΓΓΓΘ©

A. ΒψCB. ΒψEC. ΒψFD. ΒψG
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥΡ’≈ΤΥΩΥ≈ΤΘ®ΖΫΩι2ΓΔΚΎΧ“4ΓΔΚΎΧ“5ΓΔΟΖΜ®5Θ©ΒΡ≈ΤΟφ»γΆΦlΘ§ΫΪΤΥΩΥ≈Τœ¥‘»ΚσΘ§»γΆΦ2±≥Οφ≥·…œΖ≈÷Ο‘ΎΉάΟφ…œΘ°–ΓΝΝΚΆ–ΓΟς…ηΦΤΒΡ”ΈœΖΙφ‘ρ «ΝΫ»ΥΆ§ ±≥ι»Γ“Μ’≈ΤΥΩΥ≈ΤΘ§ΝΫ’≈≈ΤΟφ ΐΉ÷÷°ΚΆΈΣΤφ ΐ ±Θ§–ΓΝΝΜώ ΛΘΜΖώ‘ρ–ΓΟςΜώ ΛΘ°«κΈ ’βΗω”ΈœΖΙφ‘ρΙΪΤΫ¬πΘΩ≤ΔΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§EΘ§FΈΣΓθABCD ΒΡΕ‘Ϋ«œΏBD…œΒΡΝΫΒψΘ§«“BE=DFΘ°
«σ÷ΛΘΚAEΓΈCFΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏ![]() ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψC.
”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψC.
Θ®1Θ©«σΒψAΒΡΉχ±ξΘΜ
Θ®2Θ©Β±SΓςABC=15 ±Θ§«σΗΟ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Ψ≠ΙΐΒψCΒΡ÷±œΏ![]() ”κ≈ΉΈοœΏΒΡΝμ“ΜΗωΫΜΒψΈΣD.ΗΟ≈ΉΈοœΏ‘Ύ÷±œΏ
”κ≈ΉΈοœΏΒΡΝμ“ΜΗωΫΜΒψΈΣD.ΗΟ≈ΉΈοœΏ‘Ύ÷±œΏ![]() …œΖΫΒΡ≤ΩΖ÷”κœΏΕΈCDΉι≥…“ΜΗω–¬Κ· ΐΒΡΆΦœσΓΘ«κΫαΚœΆΦœσΜΊ¥πΘΚ»τ–¬Κ· ΐΒΡΉν–Γ÷Β¥σ”Ύ©¹8Θ§«σkΒΡ»Γ÷ΒΖΕΈß.
…œΖΫΒΡ≤ΩΖ÷”κœΏΕΈCDΉι≥…“ΜΗω–¬Κ· ΐΒΡΆΦœσΓΘ«κΫαΚœΆΦœσΜΊ¥πΘΚ»τ–¬Κ· ΐΒΡΉν–Γ÷Β¥σ”Ύ©¹8Θ§«σkΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®6Ζ÷Θ©»γΆΦΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΆχΗώ÷–ΟΩ“ΜΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ1ΗωΒΞΈΜ≥ΛΕ»ΘΜ“―÷ΣΓςABCΘ°
Θ®1Θ©Ής≥ωΓςABC“‘OΈΣ–ΐΉΣ÷––ΡΘ§Υ≥ ±’κ–ΐΉΣ90ΓψΒΡΓςA1B1C1Θ§Θ®÷ΜΜ≠≥ωΆΦ–ΈΘ©Θ°
Θ®2Θ©Ής≥ωΓςABCΙΊ”Ύ‘≠ΒψO≥…÷––ΡΕ‘≥ΤΒΡΓςA2B2C2Θ§Θ®÷ΜΜ≠≥ωΆΦ–ΈΘ©Θ§–¥≥ωB2ΚΆC2ΒΡΉχ±ξΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com