
【题目】(6分)如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1,(只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2,(只画出图形),写出B2和C2的坐标.

科目:初中数学 来源: 题型:
【题目】同学们,在初一学习正多边形和圆这节课时,我们就学习过四边形的内角和等于360°.下面我们就在四边形中来研究几个问题:
(1)问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是______;
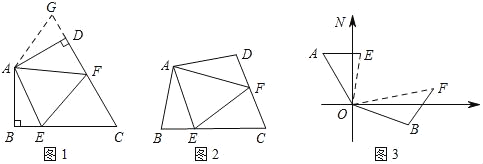
(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍成立,并说明理由;
∠BAD,上述结论是否仍成立,并说明理由;
(3)实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(点O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以45海里/时的速度前进,同时,舰艇乙沿北偏西50°的方向以60海里/时的速度前进,2小时后,指挥中心观察到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2-4ax+b交x轴正半轴于A,B两点,交y轴正半轴于C,且OB=OC=3.
(1)求抛物线的解析式;
(2)点D为抛物线的顶点,点G在直线BC上,若![]() ,直接写出点G的坐标;
,直接写出点G的坐标;
(3)将抛物线向上平移m个单位,交BC于点M,N(如图2),若∠MON=45°,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() a2b)2(﹣9ab)÷(-
a2b)2(﹣9ab)÷(-![]() a3b2);
a3b2);
(2)(x+2y)(x﹣2y)﹣(x+y)(x﹣y);
(3)[(2a+b)2﹣(a﹣b)(3a﹣b)﹣a]÷(﹣![]() a),其中a=﹣1,b=
a),其中a=﹣1,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
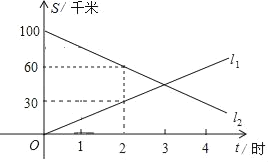
【题目】A,B两地相距100千米,甲,乙两人骑车同时分别从A、B两地相向而行,假设他们都保持匀速行驶,直线l1,l2分别表示甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间关系的图象.
根据图象提供的信息,解答下列问题:
(1)甲、乙两人的速度分别是多少?
(2)经过多长时间,两人相遇?
(3)分别写出甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
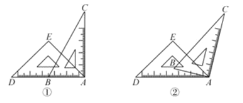
【题目】一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0)、B(3,-1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2: 1在位似中心的异侧将△OBC放大为![]() ,放大后点B、C两点的对应点分别为
,放大后点B、C两点的对应点分别为![]() 、
、![]() ,画出
,画出![]() ,并写出点为
,并写出点为![]() 、
、![]() 的坐标。
的坐标。
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点![]() 的坐标。(3)求
的坐标。(3)求![]() 的面积。
的面积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com