
【题目】一个不透明的袋子中装有分别标注着汉字“海、“棠”、“园”的三个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一球,球上的汉字恰好是“园”的概率是
(2)若从袋中任取一球,记下汉字后放回袋中,然后再从中任取一球,再次记下球上的汉字,求两次的汉字恰好组成“海棠”这个词的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
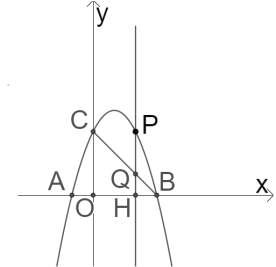
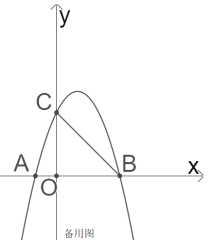
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C(0,3),点P是抛物线在第一象限上的一点,过点P作PH⊥x轴,垂足为H,交线段BC于点Q.
(1)求抛物线对应的函数表达式;
(2)当PQ=2QH时,求点P的坐标;
(3)当PH最大时,连接AP,AP与BC交于点D,点F是第一象限内一点,且∠AFC=45°,点G在抛物线上,直线FG、FC分别与直线PH交于点M、N.当三角形ABD相似三角形FMN时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 为线段
为线段![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),连接
重合),连接![]() ,作
,作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
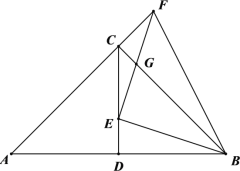
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.若乙比甲的水位高2cm时,注水时间m分钟,则m的值为( )

A.3或5B.4或6C.3或![]() D.5或9
D.5或9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com