
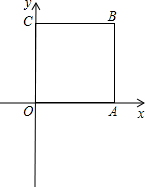 如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.
如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.| 2-m |
| 3 |
| m |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
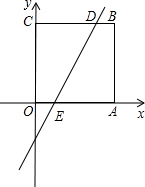
| 2-m |
| 3 |
| m |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| m |
| 3 |
| 2-m |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
| m |
| 3 |
| 2-m |
| 3 |
| 8 |
| 3 |


科目:初中数学 来源: 题型:
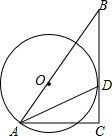 如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D
如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D查看答案和解析>>
科目:初中数学 来源: 题型:
 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A.为了集中光线,加上了灯罩,如图所示.已知灯罩深8cm,灯泡离地面2m,为了使光线恰好照在墙角,则灯罩的直径应为多少(DE、GF分别为地面与天花板的对角线.计算结果精确到0.01m)?
在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A.为了集中光线,加上了灯罩,如图所示.已知灯罩深8cm,灯泡离地面2m,为了使光线恰好照在墙角,则灯罩的直径应为多少(DE、GF分别为地面与天花板的对角线.计算结果精确到0.01m)?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
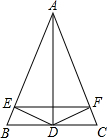 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠BAD=∠CAD;(2)ED=FD;(3)AD平分∠EDF;(4)AD,EF互相垂直平分.其中正确的有( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠BAD=∠CAD;(2)ED=FD;(3)AD平分∠EDF;(4)AD,EF互相垂直平分.其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com