
【题目】如图,在△ABC中,∠ABC=90°,BC=6,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BH的长;
(2)若AB=12,试判断∠CBD与∠A的数量关系,请说明理由.
【答案】
(1)解:∵DH∥AB,
∴△ABC∽△DHC,
∴ ![]() ,
,
∵BC=6,AC=3CD,
∴CH=2,
∴BH=BC+CH=6+2=8;
(2)解:∠CBD=∠A,
理由是:∵AC=3CD,△ABC∽△DHC,
∴ ![]() =3,
=3,
∵AB=12,
∴DH=4,
∵DH∥AB,∠ABC=90°,
∴∠ABC=∠H=90°,
∵AB=12,BC=6,BH=8,DH=4,
∴tan∠CND= ![]() ,tanA=
,tanA= ![]() ,
,
∴∠CBD=∠A.
【解析】(1)由已知条件DH∥AB,得出△ABC∽△DHC,再得对应边成比列,建立方程,即可求出BH的长。
(2)先由△ABC∽△DHC,得出对应边成比例,求出AB的长,再证明∠H=90°,然后利用三角函数的定义分别求出tan∠CND,tanA的值,即可得出∠CBD与∠A的数量关系。
【考点精析】本题主要考查了平行线的性质和相似三角形的判定的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某市计划在城区投放一批“共享单车”,这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)在“共享单车”试点,投放A,B两种款型的单车共100辆,总价值36 800元.试问本次试点投放的A型车与B型车各多少辆?
设本次试点投放的A型车![]() 辆、B型车
辆、B型车![]() 辆.
辆.
根据题意,列方程组___________
解这个方程组,得___________
答: .
(2)该市决定在整个城区投放 “共享单车”.按照(Ⅰ)中试点投放A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问整个城区投放的A型车至少多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)如图②,点G在BE上,且∠BDG=∠C.求证:△DEG∽△ECF;
(3)在(2)的条件下,已知EF=2,CE=3,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
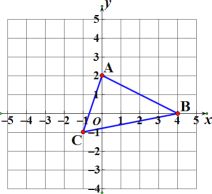
【题目】如图,在边长为 1 的正方形网格中,三角形 ABC 中任意一点 P(x0,y0)经平移后对应点为 P1(x0-4,y0+3),已知 A(0,2),B(4,0),C(-1,-1),将三角形 ABC 作同样的平移得到三角形 A1B1C1
(1)直接写出坐标:A1( , ),B1( , ),C1( , );
(2)三角形 A1B1C1 的面积为 ;
(3)已知点 P 在 y 轴上,且三角形 PAC 的面积等于三角形 ABC 面积的一半,求 P 点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),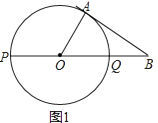
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);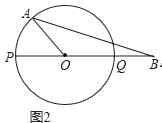
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).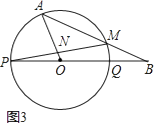
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:A( , )、B( , );
(2)求△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′,写出A′、B′、C′三个点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能找出规律吗?
(1)计算:![]() = ,
= , ![]() = ,
= ,![]() = ,
= ,![]() = .
= .
(2)请按找到的规律计算:![]() ;
;
(3)已知:a=![]() ,b=
,b=![]() ,则
,则![]() = (用含a、b的式子表示).
= (用含a、b的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com