
【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)如图②,点G在BE上,且∠BDG=∠C.求证:△DEG∽△ECF;
(3)在(2)的条件下,已知EF=2,CE=3,求GE的长.
【答案】
(1)证明:∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEB=∠C,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,又∠DEB=∠C,
∴△DEG∽△ECF;
(3)解:∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴ ![]() ,即BD2=BEBG,
,即BD2=BEBG,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM,
又∵DM=AD,AD=BD,
∴EF=BD=2,
∵BE=CE,EF=2,CE=3,
∴22=3BG,
∴BG= ![]() ,
,
∴GE=3﹣ ![]() =
= ![]() .
.
【解析】(1)(1)根据DM∥EF得到∠AMD=∠AFE,等量代换得到∠AMD=∠A,根据等角对等边证明即可。
(2)根据三角形中位线定理得到DE∥AC,证得∠BDE=∠AFE,再根据∠BDG+∠GDE=∠C+∠FEC,证明∠GDE=∠FEC,根据相似三角形的判定定理证明。
(3)根据已知易证△BDG∽△BED,得到BD2=BEBG,再证明四边形DEFM是平行四边形,从而求出BD、BE的长,即可求得BG的长,继而得出GE的长。
【考点精析】本题主要考查了平行线的性质和三角形中位线定理的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]()
(1)该抛物线的对称轴是 , 顶点坐标;
(2)选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;
x | … | … | |||||
y | … | … |

(3)若该抛物线上两点A(x1 , y1),B(x2 , y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点G作GP∥AB.则下列结论:①∠AMF与∠DNF是对顶角;②∠PGM=∠DNF;③∠BMN+∠GHN=90°;④∠AMG+∠CHG=270°.其中正确结论的个数( )
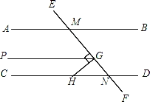
A.1个B.2 个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究活动)
(1)问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.

请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= (等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,试探究∠B、∠C、∠BEC的数量关系并证明;
(3)解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(直接写出结论,不用写计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:![]() ,其中x=﹣
,其中x=﹣![]() .
.
(2)小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
①用含x、y的代数式表示厨房的面积是_____m2;卧室的面积是______m2
②写出用含x、y的代数式表示这套房的总面积是多少平方米?
③当x=3,y=2时,求这套房的总面积是多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a ![]() ,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)求点P(﹣2,3)的“2关联点”P′的坐标;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,6),求出k及点P的坐标;
(3)如图,点Q的坐标为(0,4 ![]() ),点A在函数y=﹣
),点A在函数y=﹣ ![]() (x<0)的图象上运动,且点A是点B的“﹣
(x<0)的图象上运动,且点A是点B的“﹣ ![]() 关联点”,当线段BQ最短时,求B点坐标.
关联点”,当线段BQ最短时,求B点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=6,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BH的长;
(2)若AB=12,试判断∠CBD与∠A的数量关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com