

分析 (1)先求出调查总人数,再求出户外活动时间为1.5小时的人数,作图即可;
(2)先求出每名学生户外活动的平均时间,再乘以总人数即可.
解答 解:(1)调查人数=10÷20%=50(人);
户外活动时间为1.5小时的人数:50×24%=12(人);
补全条形图,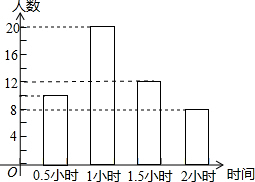
(2)每名学生户外活动的平均时间为:$\frac{10×0.5+20×1+12×1.5+8×2}{50}$=1.18(小时),
2000×1.18=2360(小时).
故根据以上调查结果估计该校全体学生每天参与户外活动所用的总时间为2360小时.
点评 本题主要考查了条形统计图,扇形统计图及用样本估计总体,解题的关键是读懂统计图,能正确的从统计图中获取信息.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
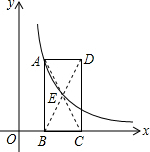 已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
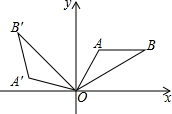 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )| A. | (-2,2$\sqrt{2}$) | B. | (-2$\sqrt{2}$,2) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
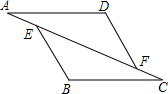 如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.
如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )| A. | △AEF≌△CED | B. | CF=AD | C. | AF=CD | D. | BF=CF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com