
甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),并根据该实验写出一个发生概率与(1)所求概率相同的事件.
解:(1)从中选出两位同学打第一场比赛所有可能出现的结果有:
| 第二位 第一位 | 甲 | 乙 | 丙 | 丁 |
| 甲 | —— | (甲,乙) | (甲,丙 | (甲,丁) |
| 乙 | (乙,甲) | —— | (乙,丙) | (乙,丁) |
| 丙 | (丙,甲) | (丙,乙) | —— | (丙,丁) |
| 丁 | (丁,甲) | (丁,乙) | (丁,丙) | —— |
共有12种,它们出现的可能性相同.所有的结果中,满足“恰好选中甲、乙两位同学”(记为事件A)的结果有2种,所以P(A)= =
=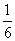 .………………4分
.………………4分
(2)本题答案不唯一,下列解法供参考.
法一:在不透明的袋中,放入2个红色1个白色3个乒乓球,它们除颜色外都一样,摇匀.第一次摸出1个球,不放回;第二次摸出1个球记下颜色,放回;第3次摸出1个球.则三次摸出的球都是红色球的概率.……………7分
法二:在不透明的袋子中,放入四个除颜色外完全一样的乒乓球,它们的颜色分别为红、黄、蓝、黑,摇匀.第一次摸出一个球后,不放回;再从袋中摸出一个球.则两次摸出的球是一红一黄的概率.……………7分
法三:在不透明的袋子中,放入2个红色2个白色共4个乒乓球.它们除颜色外都一样,摇匀.连续摸2次不放回,则两次摸到的球都是红色球的概率.………7分
法四:在不透明的袋子中,放入编号为1、2、3、4、5、6的6个乒乓球,它们除编号外其它都一样,摇匀.第一次摸出1个球记下颜色后放回;第二次摸出1个球.则两次摸出颜色相同的球的概率.……………7分


科目:初中数学 来源: 题型:
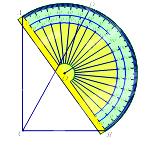
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A. 27° B. 54° C.63° D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
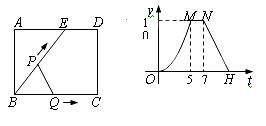
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE—ED—DC运动到点C时停止,点Q沿BC运动到点C时停止 ,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:AD=BE=5;cos∠ABE=
,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:AD=BE=5;cos∠ABE=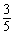 ;当0<t≤5时,y=
;当0<t≤5时,y=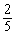 t2;当t=
t2;当t=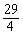 秒时,△ABE∽△QBP;其中正确的结论是_ __(填序号).
秒时,△ABE∽△QBP;其中正确的结论是_ __(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
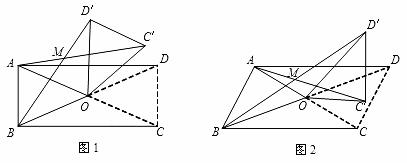
在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB =α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知在△ABC中,AC=3,BC=4,∠C=90°,建立以点A为坐标原点,使 AB落在x轴的负半轴上的平面直角坐标系,则点C的坐标为( )
AB落在x轴的负半轴上的平面直角坐标系,则点C的坐标为( )
A. 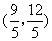 或
或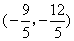 B.
B.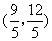 或
或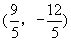
C.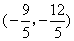 或
或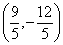 D.
D. 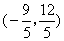 或
或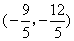
查看答案和解析>>
科目:初中数学 来源: 题型:
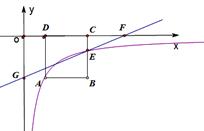
如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数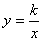 (k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,
(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n, ),过点E的直线
),过点E的直线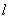 交x轴
交x轴
于点F,交y轴于点G(0,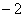 ),则点F的坐标是 .
),则点F的坐标是 .
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com