
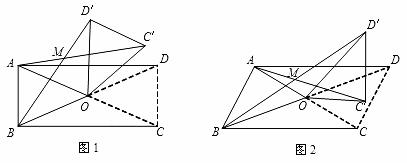
在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB =α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
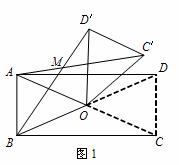
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
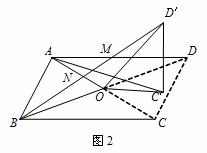
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
(1)证明:在矩形ABCD中,
∵AC=BD,OA=OC=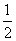 AC,OB=OD=
AC,OB=OD=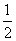 BD,
BD,
∴OA=OC=OB=OD,
∵△D′OC′由△DOC旋转得到,
∴OD=OD′,OC=OC′,∠D′OD=∠C′OC,
∴OB=OD′=OA=OC′,…………1分
∴180°-∠D′OD=180°-∠C′OC,
即∠BOD′=∠AOC′,…………2分
∴△BOD′≌△AOC′…………3分
(2)①猜想:△BOD′∽△AOC′.
证明:在平行四边形ABCD中,OB=OD,OA=OC,
∵△D′OC′由△DOC旋转得到,
∴OD=OD′,OC=OC′,∠D′OD=∠C′OC,
∴OB:OA=OD′:OC′,…………4分
180°-∠D′OD=180°-∠C′OC,
∴∠BOD′=∠AOC′,…………5分
∴△BOD′∽△AOC′…………6分
②结论:AC′=kBD′,∠AMB=α
证明:∵△BOD′∽△AOC′,
∴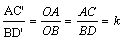 ,即AC′=kBD′ …………7分
,即AC′=kBD′ …………7分
设BD′与AC相交于点N,∵△BOD′∽△AOC′,∴∠OBM=∠OAM,
在△ANM与△BNO中,又∵∠ANM=∠BNO,
∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO,
即∠AMB=∠AOB=α.………………9分


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
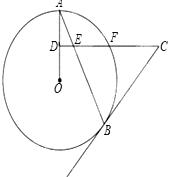
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA=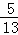 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c(a≠0)的部分对应值如下表:
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
则二次函数y=ax2+bx+c在x=2时,y=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),并根据该实验写出一个发生概率与(1)所求概率相同的事件.
查看答案和解析>>
科目:初中数学 来源: 题型:
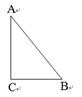
如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P 的位置应在( )
A.AB中点 B.BC中点
C.AC中点 D.∠C的平分线与 AB的交点
AB的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
.规定新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-2]的一次函数是正比例函数,则关于x的方程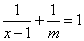 的解为………………………………………………………………………………………【 】
的解为………………………………………………………………………………………【 】
A.1 B. 2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
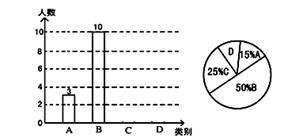
某校实施课堂教学改革后, 学生的自主学习、合作交流能力有了很大提高.九(2)班的陈老师为了解本班学生自主学习、合作交流的具体情况,对部分同学进行了一段时间的跟踪调查,将调查结果(分为A:特别好;B:好;C:一般;D:较差四类)绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
学生的自主学习、合作交流能力有了很大提高.九(2)班的陈老师为了解本班学生自主学习、合作交流的具体情况,对部分同学进行了一段时间的跟踪调查,将调查结果(分为A:特别好;B:好;C:一般;D:较差四类)绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1) 本次调查中,陈老师一共调查了 名同学,并补全条形统计图;
(2) 扇形统计图中,D类所占圆心角为 度;
(3) 为了共同进步,陈老师想从被调查的A类(1名男生2名女生)和D类(男女生各占一半)
中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两
位同学恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com