
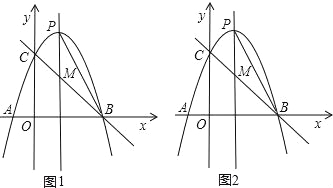
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0).
(1)求b、c.
(2)如图1,在第一象限内的抛物线上是否存在点D,使得三角形BCD的面积最大?若存在,求出D点坐标,求出三角形BCD的面积最大值;若不存在,请说明理由.
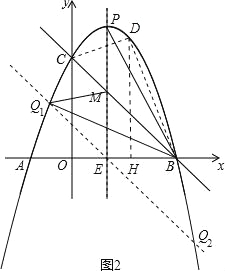
(3)如图2,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=-x2+2x+3;(2)(![]() ,
,![]() ),
),![]() ;(3)Q1(
;(3)Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,-
,-![]() )
)
【解析】
试题分析:(1)把A(-1,0)、B(3,0)两点代入y=-x2+bx+c,即可求出抛物线的解析式;
(2)设D点坐标为(t,-t2+2t+3),过点D作DH⊥x轴于H,根据![]() =-
=-![]() t2+
t2+![]() t,再利用配方法即可求出D点坐标及△BCD面积的最大值;
t,再利用配方法即可求出D点坐标及△BCD面积的最大值;
(3)设PM与x轴交于点E,求出过点E与BC平行的直线EQ解析式为y=﹣x+1,解方程组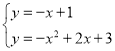 ,即可得出点Q的坐标.
,即可得出点Q的坐标.
试题解析:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)如图1,设D点坐标为(t,﹣t2+2t+3),过点D作DH⊥x轴于H,
则![]() =
=![]() (﹣t2+2t+3+3)t+
(﹣t2+2t+3+3)t+![]() (3﹣t)(﹣t2+2t+3)﹣
(3﹣t)(﹣t2+2t+3)﹣![]() ×3×3
×3×3
=﹣![]() t2+
t2+![]() t
t
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=![]() 时,D点坐标是(
时,D点坐标是(![]() ,
,![]() ),△BCD面积的最大值是
),△BCD面积的最大值是![]() ;
;
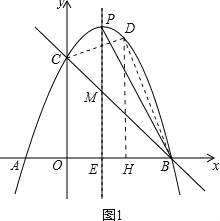
(3)如图2,设PM与x轴交于点E,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴P点的坐标为(1,4),E点的坐标为(1,0).
∵B(3,0),C(0,3),
∴直线BC的解析式为y=﹣x+3,
∴当x=1时,y=2,
∴M点的坐标为(1,2),
∴PM=ME=2,BM为△BPE的中线,
∴![]() .
.
过E作BC的平行线,交抛物线于点Q,则![]() ,
,
∴![]() .
.
∵E(1,0),直线BC的解析式为y=﹣x+3,EQ∥BC,
∴直线EQ的解析式为y=﹣x+1.
由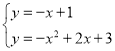 ,
,
解得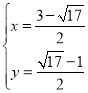 ,或
,或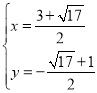 ,
,
∴点Q的坐标为Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ),
),
∴在直线BC下方的抛物线上存在点Q,使得△QMB与△PMB的面积相等,此时点Q的坐标为Q1(![]() ,
,![]() ),Q2(
),Q2(![]() ,﹣
,﹣![]() ).
).


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】利用简便方法计算:
(1)7.6×201.4+4.3×201.4-1.9×201.4 (2)![]()
(3)1072 (4)482-472 (5)102×98
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20![]() 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
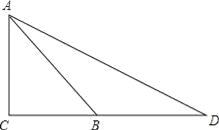
(1)求加固部分即△ABD的横截面的面积;
(2)若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在设计调查问卷时,下面的提问比较恰当的是( )
A.我认为猫是一种很可爱的动物
B.难道你不认为科幻片比武打片更有意思
C.你给我回答倒底喜不喜欢猫呢
D.请问你家有哪些使用电池的电器
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某校初二300名学生的某次数学考试成绩,现在要知道90分以上的占多少,80﹣90分占多少,70﹣80占多少,60﹣70占多少,60分以下占多少,需要做的工作是( )
A.抽取样本,需样本估计总体
B.求平均成绩
C.计算方差
D.进行频率分布
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com