
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为( )

A. 2对 B. 3对 C. 4对 D. 5对
【答案】C
【解析】
先根据条件,利用AAS可知△ADB≌△AEC,然后再利用HL、ASA即可判断△AOE≌△AOD,△BOE≌△COD,△AOC≌△AOB.
∵AB=AC,BD⊥AC于D,CE⊥AB于E,
∴∠ADB=∠AEC=90°,
∵∠A为公共角,
∴△ADB≌△AEC,(AAS)
∴AE=AD,∠B=∠C
∴BE=CD,
∵AE=AD,OA=OA,∠ADB=∠AEC=90°,
∴△AOE≌△AOD(HL),
∴∠OAC=∠OAB,
∵∠B=∠C,AB=AC,∠OAC=∠OAB,
∴△AOC≌△AOB.(ASA)
∵∠B=∠C,BE=CD,∠ODC=∠OEB=90°,
∴△BOE≌△COD(ASA).
综上:共有4对全等三角形,
故选C.


科目:初中数学 来源: 题型:
【题目】下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7 , 根据表中所提供的信息,以下判断正确的是( ).
①a>0;
②9<m<16;
③k≤9;
④b2≤4a(c﹣k).
x | … | x1 | x2 | x3 | x4 | x5 | x6 | x7 | … |
y | … | 16 | m | 9 | k | 9 | m | 16 | … |
A.①②
B.③④
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
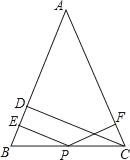
【题目】如图,在△ABC中,AB=AC,CD垂直AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F.
(1)若P为BC边中点,则PE,PF,CD三条线段有何数量关系(写出推理过程)?
(2)若P为线段BC上任意一点,则(1)中关系还成立吗?
(3)若P为直线BC上任意一点,则PE,PF,CD三条线段间有何数量关系(请直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).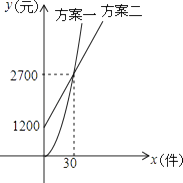
(1)分别求两种方案中y关于x的函数关系式;
(2)当销售达到多少件时,两种方案月报酬差额将达到3800元?
(3)若公司决定改进“方案二”:保持基本工资不变,每件报酬增加m元,使得当销售员销售产量达到40件时,两种方案的报酬差额不超过1000元.求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(0,6),点B的坐标是(6,0).
(1)如图1,点C的坐标是(﹣2,0),BD⊥AC于D交y轴于点E.求点E的坐标;
(2)在(1)的条件下求证:OD平分∠CDB;
(3)如图2,点F为AB中点,点G为x正半轴点B右侧一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH﹣S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=![]() +2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
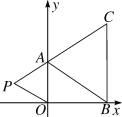
A. (-3,1) B. (-2,1) C. (-4,1) D. (-2.5,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
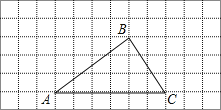
【题目】在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.
(1)过B作AC的平行线BD.
(2)作出表示B到AC的距离的线段BE.
(3)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).
(4)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )

A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com