
����Ŀ��ij��˾����һ�ֲ�Ʒ����˾��������Ա���±��������ַ�����ͼ��ʾ�����з���һ��ʾͼ���Ƕ���B��ԭ��������ߵ�һ���֣���������ʾͼ�������ߣ�������Ա������Ʒ������Ϊx����������������Ա���±���Ϊy��Ԫ����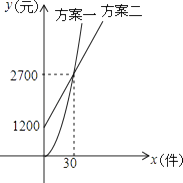
��1���ֱ������ַ�����y����x�ĺ�����ϵʽ��
��2�������۴ﵽ���ټ�ʱ�����ַ����±�����ﵽ3800Ԫ��
��3������˾�����Ľ����������������ֻ������ʲ��䣬ÿ����������mԪ��ʹ�õ�����Ա���۲����ﵽ40��ʱ�����ַ����ı��������1000Ԫ����m��ȡֵ��Χ��
���𰸡�
��1���⣺�� ![]() ���ѣ�30��2700������ã�900a=2700��
���ѣ�30��2700������ã�900a=2700��
��ã�a=3��
�� ![]() ��
��
��y2=kx+b���ѣ�0��1200������30��2700������ã� ![]() ��
��
��ã� ![]() ��
��
��y2=50x+1200��
��2���⣺������ã�30x2����50x+1200��=3800��
��ã� ![]() =50��
=50�� ![]() =
= ![]() ����ȥ����
����ȥ����
�𣺵����۴ﵽ50��ʱ�����ַ����±�����ﵽ3800Ԫ
��3���⣺������Ա���۲����ﵽ40��ʱ��
����һ���±���Ϊ����50+m����40+1200=40m+3200��
���������±���Ϊ��3��402=4800��
������ã�4800����40m+3200����1000����40m+3200��4800��1000��
��ã�15��m��65
����������1������ͼ���ϵĽ������꣨30��2700�����õ����κ�����һ�κ����Ľ���ʽ����2�����ݲ��ﵽ3800Ԫ���õ�һԪ���η��̣��õ������۴ﵽ50��ʱ�����ַ����±�����ﵽ3800Ԫ����3��������Ա���۲����ﵽ40��ʱ���������һ�ͷ������ı��꣬���ݱ��������1000Ԫ�����m��ȡֵ��Χ��


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���A��B������ֱ�Ϊ��1��5���ͣ�4��0������C��y���ϵ�һ�����㣬��A��B��C���㲻��ͬһ��ֱ���ϣ�����ABC���ܳ���Сʱ����C���������� ��
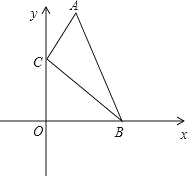
A. ��0��1�� B. ��0��2�� C. ��0��3�� D. ��0��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������������A��B��C�����Ƕ�Ӧ�����ֱ�Ϊa��b��c����c��b=b��a����C��Ӧ������10��
��1����BC=15����a��b��ֵ��
��2����ͼ2���ڣ�1���������£�OΪԭ�㣬����P��Q�ֱ��A��Cͬʱ��������P�����˶����˶��ٶ�Ϊ2����λ����/�룬��Q�����˶����˶��ٶ�Ϊ1����λ����/�룬NΪOP���е㣬MΪBQ���е㣮
���ú�t����ʽ��ʾPQ�� MN��
����P��Q���˶������У�PQ��MN����һ��ȷ���ĵ�����ϵ����ָ������֮��Ĺ�ϵ����˵�����ɣ�
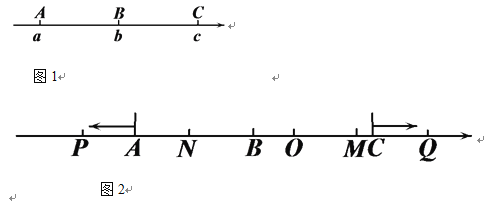
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
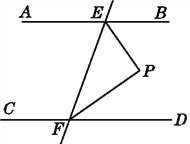
����Ŀ����ͼ,��֪AB��CD,ֱ��EF�ֱ�AB,CD�ڵ�E,F,EPƽ����BEF,FPƽ����DFE.��˵��:��PEF��ֱ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��˫����y= ![]() ��x��0���ϣ�����OA��AB����OA��ABΪ����OABC������Cǡ����˫����y=
��x��0���ϣ�����OA��AB����OA��ABΪ����OABC������Cǡ����˫����y= ![]() ��x��0���ϣ���ʱOABC�����Ϊ ��
��x��0���ϣ���ʱOABC�����Ϊ �� 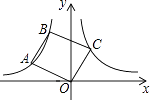
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ����м��㣺
��1�����㣺 ![]() +����2017��0��4sin45��
+����2017��0��4sin45��
��2������m��1��m��+��m��2��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��BD��AC��D��CE��AB��E��BD��CE����O������AO����ͼ�й���ȫ�������εĶ���Ϊ�� ��

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������DEF��������ABC����ij�ֱ任�õ���ͼ�Σ���A���D����B���E����C���F�ֱ��Ƕ�Ӧ�㣮�۲����������֮��Ĺ�ϵ������������⣺
(1)�ֱ�д����A���D����B���E����C���F�����꣬��˵��������DEF����������ABC���������ı任�õ��ģ�
(2)����Q(a��3��4��b)�ǵ�P(2a��2b��3)ͨ�������任�õ��ģ���a��b��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��y����һ��������T���涨��T��x��y����![]() ������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�����������㣬���磺T��0��1����
������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�����������㣬���磺T��0��1����![]() ��b����֪T��1��1����2.5��T��4����2����4��
��b����֪T��1��1����2.5��T��4����2����4��
��1����a��b��ֵ��
��2��������m�IJ���ʽ��![]() ǡ����2�������⣬��ʵ��P��ȡֵ��Χ��
ǡ����2�������⣬��ʵ��P��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com