
【题目】在平面直角坐标系中,点A的坐标是(0,6),点B的坐标是(6,0).
(1)如图1,点C的坐标是(﹣2,0),BD⊥AC于D交y轴于点E.求点E的坐标;
(2)在(1)的条件下求证:OD平分∠CDB;
(3)如图2,点F为AB中点,点G为x正半轴点B右侧一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH﹣S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.

【答案】(1)点E的坐标为(0,2);(2)详见解析;(3)S△AFH﹣S△FEG=9不发生变化,理由详见解析.
【解析】
(1)易得OA=OB,由∠ACO+∠CAO=90°,∠BCD+∠CBE=90°,可得∠CAO=∠CBE,可证得△AOC≌△BOE,可得OE=OC,可得E点左边;
(2)过点O作OM⊥BD于M,ON⊥AC于N,由△AOC≌△BOE,可得S△AOC=S△BOE,由AC=BE,可得OM=ON,所以点O一定在∠CDB的角平分线上,即OD平分∠CDB;
(3))S△AFH﹣S△FEG=9不发生变化,理由如下:连接OF,可证得△FOH≌△FBG,可得
S△AOC=S△BOE,可得S△AFH﹣S△FBG=S△AFH﹣S△FOH=S△FOA=![]() =9.
=9.
解:(1)∵x轴⊥y轴
∴∠AOC=∠BOE=90°
∴∠ACO+∠CAO=90°
∵BD⊥AC
∴∠BCD+∠CBE=90°
∴∠CAO=∠CBE,
∵点A,B的坐标分别为(0,6),(6,0)
∴OA=OB=6,
在△AOC和△BOE中
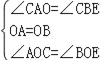
∴△AOC≌△BOE(ASA)
∴OE=OC,
∵点C的坐标为(﹣2,0)
∴OC=OE=2
∴点E的坐标为(0,2)
(2)过点O作OM⊥BD于M,ON⊥AC于N

∵△AOC≌△BOE
∴S△AOC=S△BOE,AC=BE,
∴![]() ACON=
ACON=![]() BCOM
BCOM
∴OM=ON,
∴点O一定在∠CDB的角平分线上
即OD平分∠CDB;
(3)S△AFH﹣S△FEG=9不发生变化,理由如下:
连接OF
∵△AOB是等腰直角三角形且点F为AB的中点
∴OF⊥AB,OF=FB,OF平分∠AOB
∴∠OFB=∠OFH+∠HFB=90°
又∵FG⊥FH
∴∠HFG=∠BFG+∠HFB=90°
∴∠OFH=∠BFG
∵∠FOB=![]()
∴∠FOH=∠FOB+∠HOB=45°+90°=135°
又∵∠FBG=180°﹣∠ABO=180°﹣45°=135°
∴∠FOH=∠FBG
在△FOH和△FBG中
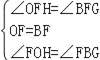
∴△FOH≌△FBG(ASA)
∴S△AOC=S△BOE
∴S△AFH﹣S△FBG
=S△AFH﹣S△FOH
=S△FOA=![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).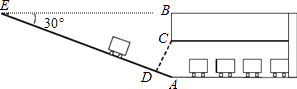
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中, ![]() 厘米,
厘米, ![]() 厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在双曲线y= ![]() (x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作OABC.若点C恰落在双曲线y= ![]() (x>0)上,此时OABC的面积为 .
(x>0)上,此时OABC的面积为 . 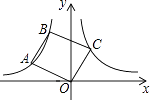
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.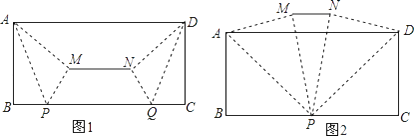
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,以D为圆心DC为半径作⊙D交AD于点G,过点G作⊙D的切线交AB于点F,且F恰好为AB中点. 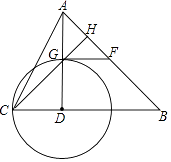
(1)求tan∠ACD的值.
(2)连结CG并延长交AB于点H,若AH=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:李华是一个勤奋好学的学生,他常常通过书籍、网络等渠道主动学习各种知识.下面是他从网络搜到的两位数乘11的速算法,其口诀是:“头尼一拉,中间相加,满十进一”.例如:①![]() .计算过程:
.计算过程:![]() 两数拉开,中间相加,即
两数拉开,中间相加,即![]() ,最后结果
,最后结果![]() ;②
;②![]() .计算过程:
.计算过程:![]() 两数分开,中间相加,即
两数分开,中间相加,即![]() ,满十进一,最后结果
,满十进一,最后结果![]() .
.
(1)计算:①![]() , ②
, ②![]() _____ ;
_____ ;
(2)若某一个两位数十位数字是![]() ,个位数字是
,个位数字是![]() ,将这个两位数乘
,将这个两位数乘![]() ,得到一个三位数,则根据上述的方法可得,该三位数百位数字是____,十位数字是_____, 个位数字是_____ ; ( 用含
,得到一个三位数,则根据上述的方法可得,该三位数百位数字是____,十位数字是_____, 个位数字是_____ ; ( 用含![]() 的化数式表示)
的化数式表示)
(3)请你结合(2)利用所学的知识解释其中原理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com