
【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.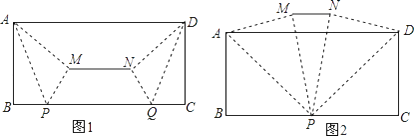
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
【答案】
(1)解:①∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD.
∵在△ABP和△DCQ中,
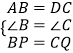 ,
,
∴△ABP≌△DCQ,
∴∠APB=∠DQG.
∴∠MPE=180°﹣2∠APB=180°﹣2∠DQC=∠NQF.
∴在△MEP和△NPQ中,
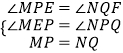 ,
,
∴△MEP≌△NPQ,
∴ME=NF;
②∵ME∥NF,ME=NF,
∴四边形EFMN是矩形,
∴MN∥BC
(2)解:延长EM、FN交AD于点G、H.
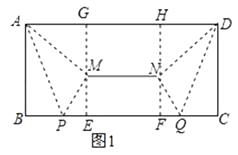
∵AB=4,BP=3,
∴AM=4,PM=3.
∵AD∥BC,
∴EM⊥AD.
∵∠AMP=∠MEP=∠MGA,
∴∠EMP=∠MAG.
∴△EMP∽△MAG.
∴ ![]() ,
,
设AG=4a,MG=3b.
∵四边形ABEG是矩形,
∴ ![]() ,
,
解得: 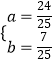 c,
c,
∴AG= ![]() ,同理DH=
,同理DH= ![]() .
.
∴MN= ![]()
(3)解:设PM、PN分别交AD于点E、F.
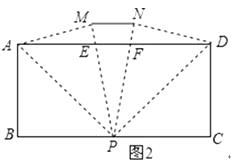
∵∠EPA=∠APB=∠PAE,
∴EA=EP.
设EA=EP=x,
在直角△AME中,42+(6﹣x)2=x2,
解得:x= ![]() .
.
∴EF=12﹣2× ![]() =
= ![]() .
.
∵EF∥MN,
∴△PEF∽△PMN.
∴ ![]() ,即
,即 ![]() ,
,
解得:MN= ![]()
【解析】(1)根据矩形的性质,四边形ABCD是矩形,得到对边相等,四角都是90°,得到△ABP≌△DCQ,△MEP≌△NPQ,得到ME=NF,MN∥BC;(2)由已知条件得到△EMP∽△MAG,得到比例,求出线段MN的长;(3)根据勾股定理求出EF的长,由EF∥MN,得到△PEF∽△PMN,得到比例,求出MN的值.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知线段AB=8,延长线段AB至C,使得BC=![]() AB,延长线段BA至D,使得AD=
AB,延长线段BA至D,使得AD=![]() AB,则下列判断正确的是 ( )
AB,则下列判断正确的是 ( )
A. BC=![]() AD B. BD=3BC C. BD=4AD D. AC=6AD
AD B. BD=3BC C. BD=4AD D. AC=6AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:
(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);
(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);
(3)将纸片收展平,那么∠AFE的度数为( )

A. 60° B. 67.5° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
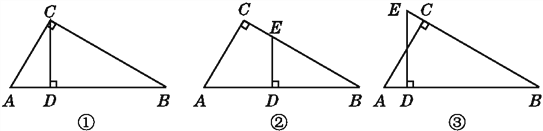
【题目】(1)如图①,CD是直角三角形ABC斜边AB上的高,图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的CD平移到ED处,图中还有与∠A相等的角吗?为什么?
(3)如图③,把图①中的CD平移到ED处,交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(0,6),点B的坐标是(6,0).
(1)如图1,点C的坐标是(﹣2,0),BD⊥AC于D交y轴于点E.求点E的坐标;
(2)在(1)的条件下求证:OD平分∠CDB;
(3)如图2,点F为AB中点,点G为x正半轴点B右侧一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH﹣S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)材料1:一般地,n个相同因数a相乘:![]() 记为
记为 ![]() 如
如![]() ,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,
,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,![]() =________;
=________;
(2)材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
①算5!=________;
②已知x为整数,求出满足该等式的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米. 
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.24,
≈2.24, ![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com