
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米. 
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.24,
≈2.24, ![]() ≈2.45)
≈2.45)
【答案】
(1)解:如图,作AD⊥BC于点D.
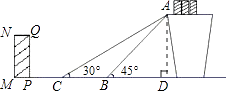
Rt△ABD中,
AD=ABsin45°=4× ![]() =2
=2 ![]() .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=4 ![]() ≈5.6.
≈5.6.
即新传送带AC的长度约为5.6米
(2)解:结论:货物MNQP应挪走.
解:在Rt△ABD中,BD=ABcos45°=4× ![]() =2
=2 ![]() .
.
在Rt△ACD中,CD=ACcos30°=2 ![]() .
.
∴CB=CD﹣BD=2 ![]() ﹣2
﹣2 ![]() =2(
=2( ![]() ﹣
﹣ ![]() )≈2.1.
)≈2.1.
∵PC=PB﹣CB≈4﹣2.1=1.9<2,
∴货物MNQP应挪走.
【解析】(1)过A作BC的垂线AD.在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.


科目:初中数学 来源: 题型:
【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.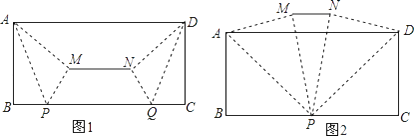
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )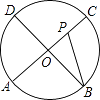
A.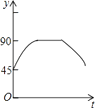
B.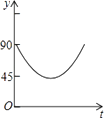
C.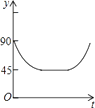
D.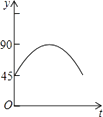
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点都在边长为1的正方形方格纸的格点上,将
的顶点都在边长为1的正方形方格纸的格点上,将![]() 向左平移2格,再向上平移4格.
向左平移2格,再向上平移4格.
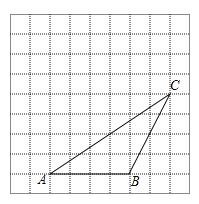
(1)在图中画出平移后的三角形![]() ;
;
(2)在图中画出三角形![]() 的高
的高![]() 、中线
、中线![]() ;
;
(3)图中线段![]() 与
与![]() 的关系是_____;
的关系是_____;
(4)![]() 的面积是_____.
的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并验证;
之间的等量关系,并验证;

(3)根据(2)题中的等量关系,解决如下问题:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:李华是一个勤奋好学的学生,他常常通过书籍、网络等渠道主动学习各种知识.下面是他从网络搜到的两位数乘11的速算法,其口诀是:“头尼一拉,中间相加,满十进一”.例如:①![]() .计算过程:
.计算过程:![]() 两数拉开,中间相加,即
两数拉开,中间相加,即![]() ,最后结果
,最后结果![]() ;②
;②![]() .计算过程:
.计算过程:![]() 两数分开,中间相加,即
两数分开,中间相加,即![]() ,满十进一,最后结果
,满十进一,最后结果![]() .
.
(1)计算:①![]() , ②
, ②![]() _____ ;
_____ ;
(2)若某一个两位数十位数字是![]() ,个位数字是
,个位数字是![]() ,将这个两位数乘
,将这个两位数乘![]() ,得到一个三位数,则根据上述的方法可得,该三位数百位数字是____,十位数字是_____, 个位数字是_____ ; ( 用含
,得到一个三位数,则根据上述的方法可得,该三位数百位数字是____,十位数字是_____, 个位数字是_____ ; ( 用含![]() 的化数式表示)
的化数式表示)
(3)请你结合(2)利用所学的知识解释其中原理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.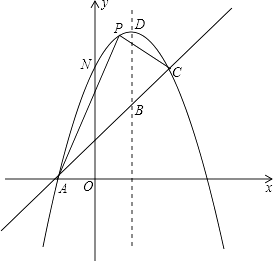
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强爱国主义教育,提高思想道德素质,某中学决定组织部分班级去山西国民师范旧址革命活动纪念馆开展红色旅游活动,在参加此次活动的师生中,若每位教师带17名学生,还剩12名学生没人带;若每位教师带18名学生,就有一位教师少带4名学生.现有甲、乙两种大客车,两种客车的载客量和租金如下表所示.
类别 | 甲种客车 | 乙种客车 |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 420 |
(1)参加此次红色旅游活动的教师和学生各有多少人?
(2)为了安全,每辆客车上要有2名教师.则怎样租车可以保证师生均有车坐,而且每辆车上都没有空座,也不超载,此时租车的费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com