【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩（得分数取正整数，满分为
分）进行统计，绘制统计图如下（未全完成），已知
组的频数比
组小
，解答下列问题：
（1）求样本容量及频数分布直方图中的
，
的值；
（2）扇形统计图中，
部分所对的圆心角为
，求
的值并补全频数分布直方图；
（3）若成绩在
分以上优秀，全校共有
名学生估计成绩优秀的学生有多少名？
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
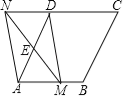
（1）求证：四边形AMDN是平行四边形．
（2）当AM的值为何值时，四边形AMDN是矩形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，点D，E，F分别在AB，BC，AC边上，且BE=CF，BD=CE．
（1）求证：△DEF是等腰三角形；
（2）当∠A=50°时，求∠DEF的度数；
（3）若∠A=∠DEF，判断△DEF是否为等腰直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，种植花卉的利润y2与投资量x的平方成正比例关系，并得到了表格中的数据．
投资量x（万元） | 2 |
种植树木利润y1（万元） | 4 |
种植花卉利润y2（万元） | 2 |
（1）分别求出利润y1与y2关于投资量x的函数关系式；
（2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在
中，
，
，
，D是AC边上的一个动点，将
沿BD所在直线折叠，使点A落在点E处．
如图
，若点D是AC的中点，连接
求证：四边形BCED是平行四边形；
如图
，若
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
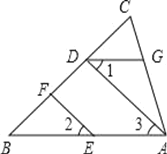
∵EF∥AD，（________）
∴∠2=______．（两直线平行，同位角相等；）
又∵∠1=∠2，（________）
∴∠1=∠3．（________）
∴AB∥DG．（________）
∴∠BAC+______=180°（________）
又∵∠BAC=70°，（________）
∴∠AGD=______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小王抽样调查了本地若干天的空气质量情况，把空气质量分成四类：
类，
类，
类和
类，分别对应的质量级别为优、良、轻度污染和中度污染四种情况，并绘制两个统计图（部分信息缺失）；
空气质量条形统计图
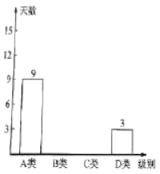
空气质量扇形统计图
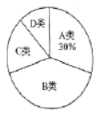
（1）本次调查的样本容量是________；
（2）已知类和类在扇形统计图中所占的夹角为
度，类的频数是类的
倍，通过计算，求出类和类的频数，并完成条形统计图；
（3）计算类在扇形统计图中所对应的圆心角度数；
（4）若一年按
天计算，求本地全年空气质量达到优良以上的天数（保留整数）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
，
，点B在x轴上，且
．
求点B的坐标；
求
的面积；
在y轴上是否存在P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑（如图①）.为了测量雕塑的高度，小明在二楼找到一点C，利用三角板测得雕塑顶端A点的仰角为
，底部B点的俯角为
，小华在五楼找到一点D，利用三角板测得A点的俯角为
（如图②）.若已知CD为10米，请求出雕塑AB的高度．（结果精确到0.1米，参考数据
）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
