
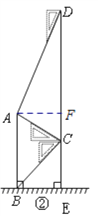
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为![]() ,底部B点的俯角为
,底部B点的俯角为![]() ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为![]() (如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() ).
).

【答案】![]()
【解析】试题分析:
由题意可得:∠ADC=30°,∠ACD=60°,∠BCE=45°,∠ABE=∠BEC=90°,由此可得∠DAC=180°-30°-60°=90°,结合CD=10可得AC=5;过点A作AF⊥DE于点F,则∠AFE=90°,从而在△AFC中由∠ACD=60°可得∠CAF=30°,由此可得CF=2.5,AF=![]() ,再证四边形ABEF是矩形可得BE=AF=
,再证四边形ABEF是矩形可得BE=AF=![]() ,结合∠BCE=45°,∠BEC=90°可得CE=BE=
,结合∠BCE=45°,∠BEC=90°可得CE=BE=![]() ,从而可得AB=EF=CF+BE=2.5+
,从而可得AB=EF=CF+BE=2.5+![]() .
.
试题解析:
由题意可得:∠ADC=30°,∠ACD=60°,∠BCE=45°,∠ABE=∠BEC=90°,
∴在△ADC中,∠DAC=180°-30°-60°=90°,
又∵CD=10,∠D=30°,
∴AC=5,
过点AF⊥CD于点F,
∴∠AFC=90°,
∵∠ACD=60°,
∴∠CAF=30°,
∴CF=2.5,AF=AC·sin60°=![]() ,
,
∵∠ABE=∠BEF=∠AFE=90°,
∴四边形ABEF是矩形,
∴BE=AF=![]() ,AB=EF,
,AB=EF,
∵在△BEC中,∠BEC=90°,∠BCE=45°,
∴CE=BE=![]() ,
,
∴AB=EF=CE+CF=2.5+![]()
![]() 6.8.
6.8.


科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为![]() 分)进行统计,绘制统计图如下(未全完成),已知
分)进行统计,绘制统计图如下(未全完成),已知![]() 组的频数比
组的频数比![]() 组小
组小![]() ,解答下列问题:
,解答下列问题:

(1)求样本容量及频数分布直方图中的![]() ,
,![]() 的值;
的值;
(2)扇形统计图中,![]() 部分所对的圆心角为
部分所对的圆心角为![]() ,求
,求![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(3)若成绩在![]() 分以上优秀,全校共有
分以上优秀,全校共有![]() 名学生估计成绩优秀的学生有多少名?
名学生估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
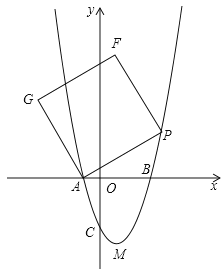
【题目】如图,在平面直角坐标系xoy中,把抛物线![]() 先向右平移1个单位,再向下平移4个单位,得到抛物线
先向右平移1个单位,再向下平移4个单位,得到抛物线![]() ,所得抛物线与x轴交于A、B两点
,所得抛物线与x轴交于A、B两点![]() 点A在点B的左边
点A在点B的左边![]() ,与y轴交于点C,顶点为M;
,与y轴交于点C,顶点为M;
![]() 写出h、k的值以及点A、B的坐标;
写出h、k的值以及点A、B的坐标;
![]() 判断三角形BCM的形状,并计算其面积;
判断三角形BCM的形状,并计算其面积;
![]() 点P是抛物线上一动点,在y轴上找点
点P是抛物线上一动点,在y轴上找点![]() 使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标
使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标![]() 不用写过程
不用写过程![]()
![]() 点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变
点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变![]() 当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标
当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标![]() 不写过程
不写过程![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.



A:踢毽子 B:乒乓球 C:篮球 D:跳绳
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,求表示区域D的扇形圆心角的度数;
(3)全校学生中喜欢篮球的人数大约是多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com