
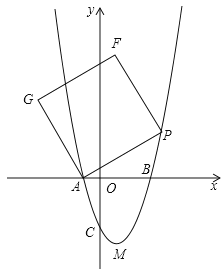
【题目】如图,在平面直角坐标系xoy中,把抛物线![]() 先向右平移1个单位,再向下平移4个单位,得到抛物线
先向右平移1个单位,再向下平移4个单位,得到抛物线![]() ,所得抛物线与x轴交于A、B两点
,所得抛物线与x轴交于A、B两点![]() 点A在点B的左边
点A在点B的左边![]() ,与y轴交于点C,顶点为M;
,与y轴交于点C,顶点为M;
![]() 写出h、k的值以及点A、B的坐标;
写出h、k的值以及点A、B的坐标;
![]() 判断三角形BCM的形状,并计算其面积;
判断三角形BCM的形状,并计算其面积;
![]() 点P是抛物线上一动点,在y轴上找点
点P是抛物线上一动点,在y轴上找点![]() 使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标
使点A,B,P,Q组成的四边形是平行四边形,直接写出对应的点P的坐标![]() 不用写过程
不用写过程![]()
![]() 点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变
点P是抛物线上一动点,连接AP,以AP为一边作正方形APFG,随着点P的运动,正方形的大小、位置也随之改变![]() 当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标
当顶点F或G恰好落在y轴上时,请直接写出对应的点P的坐标![]() 不写过程
不写过程![]()
![]()
【答案】(1)![]() ,B
,B![]() ;(2)3;(3)点P的坐标为
;(2)3;(3)点P的坐标为![]() ,
,![]() 或
或![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() 或
或![]()
【解析】
![]() 利用抛物线的平移规律即可求得h和k的值;然后令
利用抛物线的平移规律即可求得h和k的值;然后令![]() 即可求得与x轴的交点坐标;
即可求得与x轴的交点坐标;
![]() 首先求得点C和点M的坐标,然后求得BC、CM及BM的长,最后利用勾股定理逆定理判定直角三角形即可;
首先求得点C和点M的坐标,然后求得BC、CM及BM的长,最后利用勾股定理逆定理判定直角三角形即可;
![]() 分两AB为边和AB为对角线两种情况讨论计算即可.
分两AB为边和AB为对角线两种情况讨论计算即可.
![]() 分别根据当点G在y轴上时和点F在y轴上时两种情况利用
分别根据当点G在y轴上时和点F在y轴上时两种情况利用![]() ≌
≌![]() 和
和![]() ≌
≌![]() 求得点P的坐标即可.
求得点P的坐标即可.
![]() 抛物线
抛物线![]() 先向右平移1个单位,再向下平移4个单位,得到抛物线
先向右平移1个单位,再向下平移4个单位,得到抛物线![]() ,
,
![]() ,
,![]() ;
;
令![]() ,即
,即![]()
解得![]() 或
或![]() ,
,
![]() ,B
,B![]() ,
,
![]() 令
令![]() ,得
,得![]() ,
,
![]() 点C的坐标为
点C的坐标为![]() ,点M的坐标为
,点M的坐标为![]()
![]() ,
,![]() ,
,![]()
![]()
![]() 是直角三角形;
是直角三角形;
![]() ;
;
![]() 由
由![]() 知,抛物线
知,抛物线![]() ,
,
![]() 点P是抛物线上一动点,
点P是抛物线上一动点,
![]() 设
设![]() ,
,
![]() 点Q在y轴上,
点Q在y轴上,
![]() 设
设![]() ,
,
![]() ,
,![]() ,
,
![]() ,AB的中点
,AB的中点![]()
![]() 点A,B,P,Q组成的四边形是平行四边形,
点A,B,P,Q组成的四边形是平行四边形,
![]() 当AB为边时,
当AB为边时,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
Ⅰ、当![]() 时,
时,![]() ,
,
![]() ,
,
Ⅱ、当![]() 时,
时,![]() ,
,
![]()
![]() 当AB为对角线时,点M是PQ的中点,
当AB为对角线时,点M是PQ的中点,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() ,
,![]() 或
或![]() ,
,
![]() 如图
如图![]() ,
,![]() 当点G在y轴上时,
当点G在y轴上时,


由![]() ≌
≌![]() ,
,
得![]() ,得
,得![]() ,
,
![]() ,
,
得![]() ,
,
![]() ,
,![]()
![]() 如图
如图![]() ,
,

当点F在y轴上时,由![]() ≌
≌![]() ,
,
得![]() ,得
,得![]() ,
,
则![]() ,
,
得![]() ,
,![]()
故![]() 或
或![]()


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
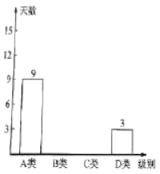
【题目】小王抽样调查了本地若干天的空气质量情况,把空气质量分成四类:![]() 类,
类,![]() 类,
类,![]() 类和
类和![]() 类,分别对应的质量级别为优、良、轻度污染和中度污染四种情况,并绘制两个统计图(部分信息缺失);
类,分别对应的质量级别为优、良、轻度污染和中度污染四种情况,并绘制两个统计图(部分信息缺失);
空气质量条形统计图
空气质量扇形统计图
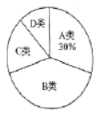
(1)本次调查的样本容量是________;
(2)已知![]() 类和
类和![]() 类在扇形统计图中所占的夹角为
类在扇形统计图中所占的夹角为![]() 度,
度,![]() 类的频数是
类的频数是![]() 类的
类的![]() 倍,通过计算,求出
倍,通过计算,求出![]() 类和
类和![]() 类的频数,并完成条形统计图;
类的频数,并完成条形统计图;
(3)计算![]() 类在扇形统计图中所对应的圆心角度数;
类在扇形统计图中所对应的圆心角度数;
(4)若一年按![]() 天计算,求本地全年空气质量达到优良以上的天数(保留整数).
天计算,求本地全年空气质量达到优良以上的天数(保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点B在x轴上,且
,点B在x轴上,且![]() .
.
![]() 求点B的坐标;
求点B的坐标;
![]() 求
求![]() 的面积;
的面积;
![]() 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
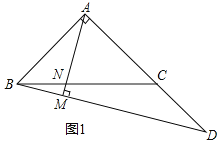
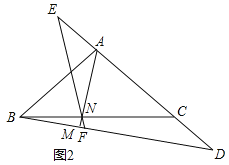
【题目】如图,在![]() 中,
中,![]() ,点D为AC延长线上一点,连接BD,过A作
,点D为AC延长线上一点,连接BD,过A作![]() ,垂足为M,交BC于点N
,垂足为M,交BC于点N
![]() 如图1,若
如图1,若![]() ,
,![]() ,求AM的长;
,求AM的长;
![]() 如图2,点E在CA的延长线上,且
如图2,点E在CA的延长线上,且![]() ,连接EN并延长交BD于点F,求证:
,连接EN并延长交BD于点F,求证:![]() ;
;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,请求出
时,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为![]() ,底部B点的俯角为
,底部B点的俯角为![]() ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为![]() (如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请画出平移后的△A'B'C',并求△A'B'C'的面积= ;
(2)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP;
(3)请在图中画出过点C且平行于AB的直线CM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com