
【题目】学校为了解全校1600名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)问:在这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.


科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲车以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙车在甲车出发2小时后匀速前往B地,比甲车早30分钟到达.到达B地后,乙车按原速度返回A地,甲车以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(小时),s与t之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为1小时;③两车在途中第二次相遇时t的值为5.25;④当t=3时,两车相距40千米,其中不正确的个数为( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在x轴上,坐标为(0,3),点B在x轴上.
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=![]() ,求点M的坐标.
,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.

(1)作出△ABC关于y轴对称的△A1B1C1,其中点A,B,C分别和点A1,B1,C1对应;
(2)平移△ABC,使得点A在x轴上,点B在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中点A,B,C分别和点A2,B2,C2对应;
(3)直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
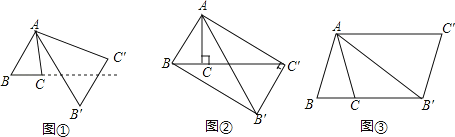
(1)如图①,对△ABC作变换[60°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com