
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΝΨΤϊ≥Β―ΊΆ§“Μ¬ΖœΏ¥”AΒΊ«ΑΆυBΒΊΘ§ΦΉ≥Β“‘a«ßΟΉ/ ±ΒΡΥΌΕ»‘»ΥΌ–– ΜΘ§ΆΨ÷–≥ωœ÷Ι ’œΚσΆΘ≥ΒΈ§–όΘ§–όΚΟΚσ“‘2a«ßΟΉ/ ±ΒΡΥΌΕ»ΦΧ–χ–– ΜΘΜ““≥Β‘ΎΦΉ≥Β≥ωΖΔ2–Γ ±Κσ‘»ΥΌ«ΑΆυBΒΊΘ§±»ΦΉ≥Β‘γ30Ζ÷÷”ΒΫ¥οΘ°ΒΫ¥οBΒΊΚσΘ§““≥ΒΑ¥‘≠ΥΌΕ»ΖΒΜΊAΒΊΘ§ΦΉ≥Β“‘2a«ßΟΉ/ ±ΒΡΥΌΕ»ΖΒΜΊAΒΊΘ°…ηΦΉΓΔ““ΝΫ≥Β”κAΒΊœύΨύsΘ®«ßΟΉΘ©Θ§ΦΉ≥ΒάκΩΣAΒΊΒΡ ±ΦδΈΣtΘ®–Γ ±Θ©Θ§s”κt÷°ΦδΒΡΚ· ΐΆΦœσ»γΆΦΥυ ΨΘ°œ¬Ν–ΥΒΖ®ΘΚΔΌa=40ΘΜΔΎΦΉ≥ΒΈ§–όΥυ”Ο ±ΦδΈΣ1–Γ ±ΘΜΔέΝΫ≥Β‘ΎΆΨ÷–ΒΎΕΰ¥Έœύ”ω ±tΒΡ÷ΒΈΣ5.25ΘΜΔήΒ±t=3 ±Θ§ΝΫ≥ΒœύΨύ40«ßΟΉΘ§Τδ÷–≤Μ’ΐ»ΖΒΡΗω ΐΈΣΘ®ΓΓΓΓΘ©

A. 0Ηω B. 1Ηω C. 2Ηω D. 3Ηω
ΓΨ¥πΑΗΓΩA
ΓΨΫβΈωΓΩ
ΫβΘΚΔΌ”…Κ· ΐΆΦœσΘ§ΒΟa=120Γ¬3=40Θ§
Ι ΔΌ’ΐ»ΖΘ§
ΔΎ”…Χβ“βΘ§ΒΟ5.5©¹3©¹120Γ¬Θ®40ΓΝ2Θ©Θ§
=2.5©¹1.5Θ§
=1Θ°
ΓύΦΉ≥ΒΈ§–όΒΡ ±ΦδΈΣ1–Γ ±ΘΜ
Ι ΔΎ’ΐ»ΖΘ§
Δέ»γΆΦΘΚ

ΓΏΦΉ≥ΒΈ§–όΒΡ ±Φδ «1–Γ ±Θ§
ΓύBΘ®4Θ§120Θ©Θ°
ΓΏ““‘ΎΦΉ≥ωΖΔ2–Γ ±Κσ‘»ΥΌ«ΑΆυBΒΊΘ§±»ΦΉ‘γ30Ζ÷÷”ΒΫ¥οΘ°
ΓύEΘ®5Θ§240Θ©Θ°
Γύ““–– ΜΒΡΥΌΕ»ΈΣΘΚ240Γ¬3=80Θ§
Γύ““ΖΒΜΊΒΡ ±ΦδΈΣΘΚ240Γ¬80=3Θ§
ΓύFΘ®8Θ§0Θ©Θ°
…ηBCΒΡΫβΈω ΫΈΣy1=k1t+b1Θ§EFΒΡΫβΈω ΫΈΣy2=k2t+b2Θ§”…ΆΦœσΒΟΘ§
![]() Θ§
Θ§![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§![]() Θ§
Θ§
Γύy1=80t©¹200Θ§y2=©¹80t+640Θ§
Β±y1=y2 ±Θ§
80t©¹200=©¹80t+640Θ§
t=5.25Θ°
ΓύΝΫ≥Β‘ΎΆΨ÷–ΒΎΕΰ¥Έœύ”ω ±tΒΡ÷ΒΈΣ5.25–Γ ±Θ§
Ι ≈ΣΔέ’ΐ»ΖΘ§
ΔήΒ±t=3 ±Θ§ΦΉ≥Β––ΒΡ¬Ζ≥ΧΈΣΘΚ120kmΘ§““≥Β––ΒΡ¬Ζ≥ΧΈΣΘΚ80ΓΝΘ®3©¹2Θ©=80kmΘ§
ΓύΝΫ≥ΒœύΨύΒΡ¬Ζ≥ΧΈΣΘΚ120©¹80=40«ßΟΉΘ§
Ι Δή’ΐ»ΖΘ§
Ι ―ΓΘΚAΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
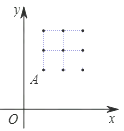
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξΒΎ÷–”–“ΜΗω2ΓΝ2ΒΡ’ΐΖΫ–ΈΆχΗώΘ§ΟΩΗωΗώΒψΒΡΚαΓΔΉίΉχ±ξΨυΈΣ’ϊ ΐΘ§“―÷ΣΒψA(1Θ§2)Θ°Ής÷±œΏOA≤Δœρ”“ΤΫ“ΤkΗωΒΞΈΜΘ§“Σ ΙΖ÷≤Φ‘ΎΤΫ“ΤΚσΒΡ÷±œΏΝΫ≤ύΒΡΗώΒψ ΐœύΆ§Θ§‘ρkΒΡ÷ΒΈΣΘ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ“Μ¥ΈΚ· ΐy=2x+a”κy=Θ≠x+bΒΡΆΦœσΕΦΨ≠ΙΐΒψA(Θ≠2Θ§0)«“”κy÷αΖ÷±πΫΜ”ΎBΘ§CΝΫΒψ

(1)Ζ÷±π«σ≥ω’βΝΫΗω“Μ¥ΈΚ· ΐΒΡΫβΈω Ϋ
(2)«σΓςABCΒΡΟφΜΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΝΫ’ΐΖΫ–Έ±Υ¥ΥœύΝΎ«“ΡΎΫ””ΎΑκ‘≤Θ§»τ–Γ’ΐΖΫ–ΈΒΡΟφΜΐΈΣ16cm2Θ§‘ρΗΟΑκ‘≤ΒΡΑκΨΕΈΣΘ®Θ©

A. ![]() cm B. 9 cm
cm B. 9 cm
C. ![]() cm D.
cm D. ![]() cm
cm
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§DΈΣBC±Ώ…œ“ΜΗωΕ·ΒψΘ®D”κBΓΔCΨυ≤Μ÷ΊΚœΘ©Θ§AD=AEΘ§ΓœDAE=60ΓψΘ§Ν§Ϋ”CEΘ°
Θ®1Θ©«σ÷ΛΘΚΓςABDΓ’ΓςACEΘΜ
Θ®2Θ©»τAB=2Θ§Β±ΥΡ±Ώ–ΈADCEΒΡ÷ή≥Λ»ΓΉν–Γ÷Β ±Θ§«σBDΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ![]() Θ§ΒψAΓΔBΖ÷±π‘Ύ…δœΏOMΓΔON…œ(AΓΔBΨυ≤Μ”κ
Θ§ΒψAΓΔBΖ÷±π‘Ύ…δœΏOMΓΔON…œ(AΓΔBΨυ≤Μ”κ![]() ÷ΊΚœ)Θ§“‘ABΈΣ±Ώ‘ΎΓœMONΒΡΡΎ≤ΩΉςΒ»±Ώ»ΐΫ«–ΈABCΘ§Ν§Ϋ”OC.
÷ΊΚœ)Θ§“‘ABΈΣ±Ώ‘ΎΓœMONΒΡΡΎ≤ΩΉςΒ»±Ώ»ΐΫ«–ΈABCΘ§Ν§Ϋ”OC.
Θ®1Θ©»γΆΦ1Θ§Β±OA=OB ±Θ§«σ÷ΛΘΚ![]() ΤΫΖ÷
ΤΫΖ÷![]() .
.

Θ®2Θ©»γΆΦ2Θ§Β±OAΓΌOB ±Θ§ΙΐΒψCΉςCDΓΆOMΘ§CEΓΆONΘ§¥ΙΉψΖ÷±πΈΣDΓΔE.«σ÷ΛΘΚOD=OE.(ΉΔΘΚΥΡ±Ώ–ΈΒΡΡΎΫ«ΚΆΈΣ![]() )
)

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘ΎΓςABC÷–Θ§ΓœA=45ΓψΘ§AB=7Θ§![]() Θ§Ε·ΒψPΓΔDΖ÷±π‘Ύ…δœΏABΓΔAC…œΘ§«“ΓœDPA=ΓœACBΘ§…ηAP=xΘ§ΓςPCDΒΡΟφΜΐΈΣyΘ°
Θ§Ε·ΒψPΓΔDΖ÷±π‘Ύ…δœΏABΓΔAC…œΘ§«“ΓœDPA=ΓœACBΘ§…ηAP=xΘ§ΓςPCDΒΡΟφΜΐΈΣyΘ°
Θ®1Θ©«σΓςABCΒΡΟφΜΐΘΜ
Θ®2Θ©»γΆΦΘ§Β±Ε·ΒψPΓΔDΖ÷±π‘Ύ±ΏABΓΔAC…œ ±Θ§«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωΚ· ΐΒΡΕ®“ε”ρΘΜ
Θ®3Θ©»γΙϊΓςPCD «“‘PDΈΣ―ϋΒΡΒ»―ϋ»ΐΫ«–ΈΘ§«σœΏΕΈAPΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§“―÷ΣAB=ACΘ§ABΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜAB”ΎΒψNΘ§ΫΜAC”ΎΒψMΘ§Ν§Ϋ”MBΘ°
Θ®1Θ©»τΓœABC=70ΓψΘ§‘ρΓœNMAΒΡΕ» ΐ «ΓΓ ΓΓΕ»Θ°
Θ®2Θ©»τAB=8cmΘ§ΓςMBCΒΡ÷ή≥Λ «14cmΘ°
ΔΌ«σBCΒΡ≥ΛΕ»ΘΜ
ΔΎ»τΒψPΈΣ÷±œΏMN…œ“ΜΒψΘ§«κΡψ÷±Ϋ”–¥≥ωΓςPBC÷ή≥ΛΒΡΉν–Γ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―ß–ΘΈΣΝΥΫβ»Ϊ–Θ1600Οϊ―ß…ζΒΫ–Θ…œ―ßΒΡΖΫ ΫΘ§‘Ύ»Ϊ–ΘΥφΜζ≥ι»ΓΝΥ»τΗ…Οϊ―ß…ζΫχ––Έ ΨμΒς≤ιΘ°Έ ΨμΗχ≥ωΝΥΈε÷÷…œ―ßΖΫ ΫΙ©―ß…ζ―Γ‘ώΘ§ΟΩ»Υ÷ΜΡή―Γ“ΜœνΘ§«“≤ΜΡή≤Μ―ΓΘ°ΫΪΒς≤ιΒΟΒΫΒΡΫαΙϊΜφ÷Τ≥…»γΆΦΥυ ΨΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΚΆ…»–ΈΆ≥ΦΤΆΦΘ®Ψυ≤ΜΆξ’ϊΘ©Θ°
Θ®1Θ©Έ ΘΚ‘Ύ’β¥ΈΒς≤ι÷–Θ§“ΜΙ≤≥ι»ΓΝΥΕύ…ΌΟϊ―ß…ζΘΩ
Θ®2Θ©≤Ι»ΪΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®3Θ©ΙάΦΤ»Ϊ–ΘΥυ”–―ß…ζ÷–”–Εύ…Ό»Υ≥ΥΉχΙΪΫΜ≥Β…œ―ßΘ°


≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com