
【题目】如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.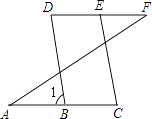
证明:∵∠A=∠F(已知)
∴AC∥()
∴∠D=∠1()
又∵∠C=∠D(已知)
∴∠1=()
∴BD∥CE()
 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
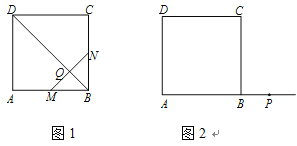
【题目】在正方形 ABCD 中,点 P 在射线 AB 上,连结 PC,PD,M,N 分别为 AB,PC 中点,连结 MN 交 PD 于点 Q.
(1)如图 1,当点 P 与点 B 重合时,求∠QMB 的度数;
(2)当点 P 在线段 AB 的延长线上时.
①依题意补全图2
②小聪通过观察、实验、提出猜想:在点P运动过程中,始终有QP=QM.小聪把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1延长BA到点 E,使AE=PB .要证QP=QM,只需证△PDA≌△ECB.
想法2:取PD 中点E ,连结NE,EA. 要证QP=QM只需证四边形NEAM 是平行四边形.
想 法3:过N 作 NE∥CB 交PB 于点 E ,要证QP=QM ,只要证明△NEM∽△DAP.
……
请你参考上面的想法,帮助小聪证明QP=QM. (一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
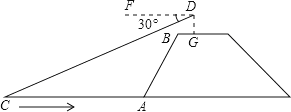
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/辆 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
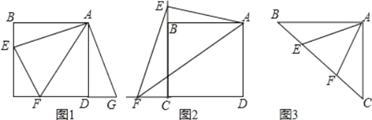
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com