
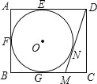
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】A
【解析】
连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=4,由于AD,AB,BC分别与⊙O相切于E,F,G三点得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=2,由勾股定理列方程即可求出结果.
连接OE,OF,ON,OG,
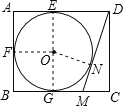
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5-2-MN=3-MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(3+NM)2=(3-NM)2+42,
∴NM=![]() ,
,
∴DM=3+![]() =
=![]() .
.
故选A.


科目:初中数学 来源: 题型:
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程.
已知:线段 a, b.

求作:等腰△ABC,使线段 a 为腰,线段 b 为底边 BC 上的高. 作法:如图,

①画直线 l,作直线 m⊥l,垂足为 P;
②以点 P 为圆心,线段 b 的长为半径画弧,交直线 m 于点 A;
③以点 A 为圆心,线段 a 的长为半径画弧,交直线 l 于 B,C 两点;
④分别连接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ = ,
∴△ABC 为等腰三角形( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
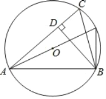
【题目】如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
A. 0.6 B. 0.8 C. ![]() D. 0.75
D. 0.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )

A、3.25m B、4.25m C、4.45m D、4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 如图1所示,BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,试说明:∠D=90°+![]() ∠A.
∠A.

(2)探究,请直接写出下列两种情况的结果,并任选一种情况说明理由:
①如图2所示,BD,CD分别是△ABC两个外角∠EBC和∠FCB的平分线,试探究∠A与∠D之间的等量关系;
②如图3所示,BD,CD分别是△ABC一个内角∠ABC和一个外角∠ACE的平分线,试探究∠A与∠D之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.

(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究.
(初步思考)
我们不妨将问题用符号语言表示为:在△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
(深入探究)
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据______,可以知道Rt△ABC≌Rt△DEF.
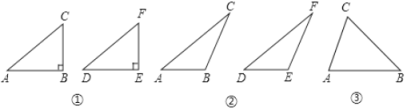
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角.求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角.请你用直尺在图③中作出△DEF,使△DEF和△ABC不全等,并作简要说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com