
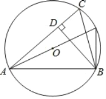
【题目】如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
A. 0.6 B. 0.8 C. ![]() D. 0.75
D. 0.75
【答案】A
【解析】
连接OA、OB,由于OM⊥AB,根据垂径定理易证得∠BOM=![]() ∠AOB,而由圆周角定理可得∠BCD=
∠AOB,而由圆周角定理可得∠BCD=![]() ∠AOB=∠BOM,因此∠CBD=∠OBM,只需求得∠OBM的正弦值即可;在Rt△OBM中,由垂径定理可得BM=4,已知⊙O的半径OB=5,由勾股定理可求得OM=3,即可求出∠OBM即∠CBD得正弦值,由此得解.
∠AOB=∠BOM,因此∠CBD=∠OBM,只需求得∠OBM的正弦值即可;在Rt△OBM中,由垂径定理可得BM=4,已知⊙O的半径OB=5,由勾股定理可求得OM=3,即可求出∠OBM即∠CBD得正弦值,由此得解.
连接OA、OB;
∵OM⊥AB,
∴AM=BM=4,∠AOM=∠BOM=![]() ∠AOB;
∠AOB;
又∵∠BCD=![]() ∠AOB,
∠AOB,
∴∠BOM=∠BCD,∠OBM=∠CBD;
在Rt△OBM中,OB=5,BM=4,由勾股定理得OM=3;
∴sin∠OBM=![]() ,sin∠CBD=sin∠OBM=
,sin∠CBD=sin∠OBM=![]() .
.
故选A.


科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长均为![]() 个单位,
个单位,![]() 的三个顶点都在格点上点.
的三个顶点都在格点上点.

(1)在网格中画出![]() 向下平移
向下平移![]() 个单位得到的
个单位得到的![]() ;
;
(2)在网格中画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(2)在直线![]() 上画一点
上画一点![]() ,使得
,使得![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标是(-1,2),且过点(0, ![]() ).
).
(1)求二次函数的解析式,并在图中画出它的图象;
(2)求证:对任意实数m,点M(m,-m2)都不在这个二次函数的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线PQ⊥直线MN,垂足为O,△AOB是直角三角形,∠AOB=90°,斜边AB与直线PQ交于点C.



(1)若∠A=∠AOC=30°,则BC_______BO(填“>”“=”“<”);
(2)如图2,延长AB交直线MN于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠AEO=α,求∠AOE的度数(用含α的代数式表示);
(3)如图3,OF平分∠AOM,∠BCO的平分线交FO的延长线于点R,∠A=36°,当△AOB绕O点旋转(斜边AB与直线PQ始终相交于点C),问∠R的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形![]() 中,
中,![]() ,将角形
,将角形![]() 绕点
绕点![]() 按逆时针方向旋转后得到三角形
按逆时针方向旋转后得到三角形![]() 在旋转过程中:
在旋转过程中:

![]() 旋转中心是什么?
旋转中心是什么?![]() 为多少度?
为多少度?
![]() 与线段
与线段![]() 相等的线段是什么?
相等的线段是什么?
![]() 三角形
三角形![]() 的面积是多少?
的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
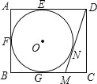
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒 传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为 了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校 学生中进行了抽样调查,根据调查结果绘制如图所示的两个不完整的统计图,请结合图中 信息解决下列问题:
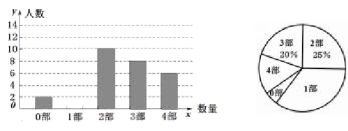
(1)请将条形统计图补充完整;
(2)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1 部”所 在扇形的圆心角为 度;
(3)若该校共有 800 个人,那么看完 3 部以上(包含 3 部)的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com