
ЁОЬтФПЁПЃЈ1ЃЉ ШчЭМ1ЫљЪОЃЌBDЃЌCDЗжБ№ЪЧЁїABCЕФФкНЧЁЯABCЃЌЁЯACBЕФЦНЗжЯпЃЌЪдЫЕУїЃКЁЯD=90Ёу+![]() ЁЯAЃЎ
ЁЯAЃЎ

ЃЈ2ЃЉЬНОПЃЌЧыжБНгаДГіЯТСаСНжжЧщПіЕФНсЙћЃЌВЂШЮбЁвЛжжЧщПіЫЕУїРэгЩЃК
ЂйШчЭМ2ЫљЪОЃЌBDЃЌCDЗжБ№ЪЧЁїABCСНИіЭтНЧЁЯEBCКЭЁЯFCBЕФЦНЗжЯпЃЌЪдЬНОПЁЯAгыЁЯDжЎМфЕФЕШСПЙиЯЕЃЛ
ЂкШчЭМ3ЫљЪОЃЌBDЃЌCDЗжБ№ЪЧЁїABCвЛИіФкНЧЁЯABCКЭвЛИіЭтНЧЁЯACEЕФЦНЗжЯпЃЌЪдЬНОПЁЯAгыЁЯDжЎМфЕФЕШСПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉЂйЁЯA=180Ёу2ЁЯDЃЌРэгЩМћНтЮіЃЛЂкЁЯA=2ЁЯDЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШРћгУНЧЦНЗжЯпаджЪЕУГіЁЯDBC=![]() ЁЯABCЃЌЁЯDCB=
ЁЯABCЃЌЁЯDCB=![]() ЁЯACBЃЌдйРћгУШ§НЧаЮФкНЧКЭЖЈРэЕУГіЁЯA+ЁЯABC+ЁЯACB=180ЁувдМАЁЯDBC+ЁЯDCB+ЁЯD=180ЁуЃЌОнДЫНјвЛВНМгвдБфаЮЧѓжЄМДПЩЃЛ
ЁЯACBЃЌдйРћгУШ§НЧаЮФкНЧКЭЖЈРэЕУГіЁЯA+ЁЯABC+ЁЯACB=180ЁувдМАЁЯDBC+ЁЯDCB+ЁЯD=180ЁуЃЌОнДЫНјвЛВНМгвдБфаЮЧѓжЄМДПЩЃЛ
ЃЈ2ЃЉЂйЪзЯШРэгЩНЧЦНЗжЯпаджЪЕУГіЁЯEBC=2ЁЯDBCЃЌЁЯFCB=2ЁЯDCBЃЌШЛКѓдйРћгУШ§НЧаЮФкНЧКЭаджЪНјвЛВНећРэЕУГіЁЯA2(ЁЯDBC+ЁЯDCB)=-180ЁуЃЌОнДЫНјвЛВНМгвдЗжЮіжЄУїМДПЩЃЛЂкРћгУШ§НЧаЮЭтНЧаджЪПЩжЊЁЯDCE=ЁЯDBC+ЁЯDЃЌШЛКѓдйРћгУНЧЦНЗжЯпаджЪЕУГі2ЁЯDBC=ЁЯABCЃЌ2ЁЯDCE=ЁЯACEЃЌзюКѓдйНсКЯЁЯA+ЁЯABC=ЁЯACEНјвЛВНжЄУїМДПЩ.
ЃЈ1ЃЉЁпBDЃЌCDЗжБ№ЪЧЁЯABCЃЌЁЯACBЕФЦНЗжЯпЃЌ
ЁрЁЯDBC=![]() ЁЯABCЃЌЁЯDCB=
ЁЯABCЃЌЁЯDCB=![]() ЁЯACBЃЌ
ЁЯACBЃЌ
ЁпЁЯA+ЁЯABC+ЁЯACB=180ЁуЃЌ
ЁрЁЯABC+ЁЯACB=180ЁуЁЯAЃЌ
гжЁпЁЯDBC+ЁЯDCB+ЁЯD=180ЁуЃЌ
ЁрЁЯD=180Ёу(ЁЯDBC+ЁЯDCB)
=180Ёу![]() (ЁЯABC+ЁЯACB)
(ЁЯABC+ЁЯACB)
=180Ёу![]() (180ЁуЁЯA)
(180ЁуЁЯA)
=180Ёу90Ёу+![]() ЁЯA
ЁЯA
=90Ёу+![]() ЁЯAЃЌ
ЁЯAЃЌ
МДЃКЁЯD=90Ёу+![]() ЁЯAЃЛ
ЁЯAЃЛ
ЃЈ2ЃЉЂйЁЯA=180Ёу2ЁЯDЃЌРэгЩШчЯТЃК
ЁпBDЃЌCDЗжБ№ЪЧЁЯEBCКЭЁЯFCBЕФЦНЗжЯпЃЌ
ЁрЁЯEBC=2ЁЯDBCЃЌЁЯFCB=2ЁЯDCBЃЌ
ЁпЁЯA+ЁЯABC+ЁЯACB=180ЁуЃЌ
ЁрЁЯABC=180Ёу(ЁЯA+ЁЯACB)=180Ёу2ЁЯDBCЃЌ
ЁЯACB=180Ёу(ЁЯA+ЁЯABC)=180Ёу2ЁЯDCBЃЌ
ЁрЁЯA+180Ёу2ЁЯDBC+180Ёу2ЁЯDCB=180ЁуЃЌ
ЁрЁЯA2(ЁЯDBC+ЁЯDCB)=180ЁуЃЌ
гжЁпЁЯDBC+ЁЯDCB+ЁЯD=180ЁуЃЌ
ЁрЁЯDBC+ЁЯDCB=180ЁуЁЯDЃЌ
ЁрЁЯA2(ЁЯDBC+ЁЯDCB)=ЁЯA2(180ЁуЁЯD)=180ЁуЃЌ
МДЃКЁЯA360Ёу+2ЁЯD=180ЁуЃЌ
Ёр2ЁЯD=180ЁуЁЯAЃЌ
МДЃКЁЯA=180Ёу2ЁЯDЃЛ
ЂкЁЯA=2ЁЯDЃЌРэгЩШчЯТЃК
ЁпЁЯDCEЪЧЁїABCЕФвЛИіЭтНЧЃЌ
ЁрЁЯDCE=ЁЯDBC+ЁЯDЃЌ
ЁпBDЃЌCDЗжБ№ЪЧЁЯABCКЭЁЯACEЕФЦНЗжЯпЃЌ
Ёр2ЁЯDBC=ЁЯABCЃЌ2ЁЯDCE=ЁЯACEЃЌ
ЁпЁЯA+ЁЯABC=ЁЯACEЃЌ
ЁрЁЯA+2ЁЯDBC=2ЁЯDCEЃЌ
ЁрЁЯA+2ЁЯDBC=2ЁЯDBC+2ЁЯDЃЌ
ЁрЁЯA=2ЁЯD.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABEжаЃЌЁЯBAEЃН105ЁуЃЌAEЕФДЙжБЦНЗжЯпMNНЛBEгкЕуCЃЌЧвABЃНCEЃЌдђЁЯBЕФЖШЪ§ЪЧ(ЁЁЁЁ)

A. 45ЁуB. 60ЁуC. 50ЁуD. 55Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпPQЁЭжБЯпMNЃЌДЙзуЮЊOЃЌЁїAOBЪЧжБНЧШ§НЧаЮЃЌЁЯAOB=90ЁуЃЌаББпABгыжБЯпPQНЛгкЕуCЃЎ



ЃЈ1ЃЉШєЁЯA=ЁЯAOC=30ЁуЃЌдђBC_______BOЃЈЬюЁАЃОЁБЁАЃНЁБЁАЃМЁБЃЉЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄABНЛжБЯпMNгкЕуEЃЌЙ§OзїODЁЭABЃЌШєЁЯDOB=ЁЯEOBЃЌЁЯAEO=ІСЃЌЧѓЁЯAOEЕФЖШЪ§ЃЈгУКЌІСЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌOFЦНЗжЁЯAOMЃЌЁЯBCOЕФЦНЗжЯпНЛFOЕФбгГЄЯпгкЕуRЃЌЁЯA=36ЁуЃЌЕБЁїAOBШЦOЕуа§зЊЃЈаББпABгыжБЯпPQЪМжеЯрНЛгкЕуCЃЉЃЌЮЪЁЯRЕФЖШЪ§ЪЧЗёЗЂЩњИФБфЃПШєВЛБфЃЌЧѓЦфЖШЪ§ЃЛШєИФБфЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌНЋНЧаЮ
ЃЌНЋНЧаЮ![]() ШЦЕу
ШЦЕу![]() АДФцЪБеыЗНЯђа§зЊКѓЕУЕНШ§НЧаЮ
АДФцЪБеыЗНЯђа§зЊКѓЕУЕНШ§НЧаЮ![]() дка§зЊЙ§ГЬжа:
дка§зЊЙ§ГЬжа:

![]() а§зЊжааФЪЧЪВУДЃП
а§зЊжааФЪЧЪВУДЃП![]() ЮЊЖрЩйЖШЃП
ЮЊЖрЩйЖШЃП
![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрЕШЕФЯпЖЮЪЧЪВУДЃП
ЯрЕШЕФЯпЖЮЪЧЪВУДЃП
![]() Ш§НЧаЮ
Ш§НЧаЮ![]() ЕФУцЛ§ЪЧЖрЩйЃП
ЕФУцЛ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=4ЃЌAD=5ЃЌADЃЌABЃЌBCЗжБ№гыЁбOЯрЧагкEЃЌFЃЌGШ§ЕуЃЌЙ§ЕуDзїЁбOЕФЧаЯпBCгкЕуMЃЌЧаЕуЮЊNЃЌдђDMЕФГЄЮЊЃЈ ЃЉ
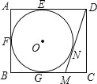
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ8ЗжЃЉФГдАСжВПУХОіЖЈРћгУЯжгаЕФ349ХшМзжжЛЈЛмКЭ295ХшввжжЛЈЛмДюХфAЁЂBСНжждАведьаЭЙВ50ИіЃЌАкЗХдкгБіДѓЕРСНВрЃЎвбжЊДюХфвЛИіAжждьаЭашМзжжЛЈЛм8ХшЃЌввжжЛЈЛм4ХшЃЛДюХфвЛИіBжждьаЭашМзжжЛЈЛм5ХшЃЌввжжЛЈЛм9ХшЃЎ
ЃЈlЃЉФГаЃ2015НьОХФъМЖФГАрПЮЭтЛюЖЏаЁзщГаНгСЫетИідАведьаЭДюХфЗНАИЕФЩшМЦЃЌЮЪЗћКЯЬтвтЕФДюХфЗНАИгаМИжжЃПЧыФуАяжњЩшМЦГіРДЃЛ
ЃЈ2ЃЉШєДюХфвЛИіAжждьаЭЕФГЩБОЪЧ200дЊЃЌДюХфвЛИіBжждьаЭЕФГЩБОЪЧ360дЊЃЌЪдЫЕУїЃЈ1ЃЉжаФФжжЗНАИГЩБОзюЕЭЃЌзюЕЭГЩБОЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
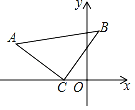
ЁОЬтФПЁПШчЭМЃЌдкЁїACBжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌЕуCЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌЕуAЕФзјБъЮЊЃЈЉ6ЃЌ3ЃЉЃЌЧѓЕуBЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ12ЗжЃЉШчЭМЃЌОиаЮABCDжаЃЌAB=8ЃЌAD=6ЃЌЕуEЁЂFЗжБ№дкБпCDЁЂABЩЯЃЎ

ЃЈ1ЃЉШєDE=BFЃЌЧѓжЄЃКЫФБпаЮAFCEЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєЫФБпаЮAFCEЪЧСтаЮЃЌЧѓСтаЮAFCEЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌжБЯпCDгывдЯпЖЮABЮЊжБОЖЕФдВЯрЧагкЕуDВЂНЛBAЕФбгГЄЯпгкЕуCЃЌЧвAB=2ЃЌAD=1ЃЌPЕудкЧаЯпCDЩЯвЦЖЏЃЎЕБЁЯAPBЕФЖШЪ§зюДѓЪБЃЌдђЁЯABPЕФЖШЪ§ЮЊЃЈ ЃЉ
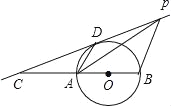
AЃЎ15Ёу BЃЎ30Ёу CЃЎ60Ёу DЃЎ90Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com