
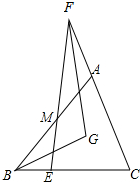
 如图,已知FG是∠EFC的角平分线,BG是∠ABC的角平分线,
如图,已知FG是∠EFC的角平分线,BG是∠ABC的角平分线,分析 (1)根据已知条件设∠MFN=∠AFN=x,∠MBG=∠EBG=y,∠AME=α,则∠FMN=∠BME=180°-α,在△BME中,根据外角的性质得到∠MEC=2y+180°-α,在△FEC中根据三角形的内角和得到∠C=180°-2x-(2y+180°-α),在△ABC中,根据三角形的内角和得到∠CAN=180°-2y-(α-2x-2y)=2x+180°-α,在△AFN中,根据外角的性质得到∠BNG═∠ANF=x+180°-α,在△BNG中根据三角形的内角和得到∠BGF=180°-y-(x+180°-α)=α-x-y,根据等式的性质即可得到结论;
(2)根据(1)的结论,代入数值即可求值.
解答 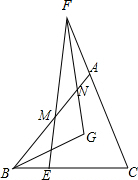 (1)证明:设∠MFN=∠AFN=x,∠MBG=∠EBG=y,∠AME=α,
(1)证明:设∠MFN=∠AFN=x,∠MBG=∠EBG=y,∠AME=α,
则:∠FMN=∠BME=180°-α,
在△BME中,∠MEC=2y+180°-α,
在△FEC中,∠AFM=2x,∠MEC=2y+180°-α,
∴∠C=180°-2x-(2y+180°-α),
在△ABC中,∠MBE=2y,∠C=α-2x-2y,
∴∠CAN=180°-2y-(α-2x-2y)=2x+180°-α,
在△AFN中,∠AFN=x,
∴∠ANF=(2x+180°-α)-x=x+180°-α,
∴∠BNG=∠ANF=x+180°-α,
在△BNG中,∠NBG=y,∠BNG-x+180°-α,
∴∠BGF=180°-y-(x+180°-α)=α-x-y,
∴$\frac{1}{2}$(∠AME+∠C)=$\frac{1}{2}$(α+α-2x-2y)=α-x-y,
∴∠BGF=$\frac{1}{2}$(∠AME+∠C);
(2)解:∵∠BGF=60°,∠FEC=80°,
∴60°-2x+2y=80°,
∴2y-2x=20°,
∴y-x=10°,
在△BNG中,∠BGF=180°-y-(60°-x)=120°+x-y,=120°-(y-x)=120°-10°=110°,
即∠BGF=110°.
点评 本题考查了三角形的内角和,角平分线性质,外角的性质,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
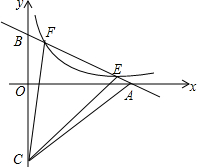 如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.
如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
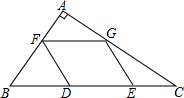 如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )
如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )| A. | AB=AC且∠A=120° | B. | △ABC为正三角形 | ||
| C. | ∠A=90° | D. | 不存在这样的三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
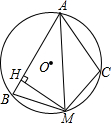 如图,⊙O的内接四边形ABMC中,AB>AC,M是$\widehat{BC}$的中点,MH⊥AB于N,求证:BH=$\frac{1}{2}$(AB-AC).
如图,⊙O的内接四边形ABMC中,AB>AC,M是$\widehat{BC}$的中点,MH⊥AB于N,求证:BH=$\frac{1}{2}$(AB-AC).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-3,-1) | C. | (1,3) | D. | ($\frac{3}{2}$,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$π | B. | $\frac{5}{3}$π+10 | C. | $\frac{5}{6}$ | D. | $\frac{5}{6}$π+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com