
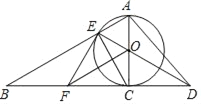
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.
(1)求证:OF⊥CE;
(2)求证:EF是⊙O的切线;
(3)若⊙O的半径为3,∠EAC=60°,求CD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,
(2)得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.
(3)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.
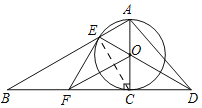
(1)如图,连接CE,
∵![]() 是
是![]() 的直径,∴
的直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
(2)∵OF⊥CE,
∴OF所在直线垂直平分CE,∴FC=FE,OE=OC,
∴∠FEC=∠FCE,∠OEC=∠OCE,
∵![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴FE为![]() 的切线.
的切线.
(3)如图,∵⊙O的半径为3,
∴AO=CO=EO=3,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵在Rt△OCD中,∠COD=60°,OC=3,∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
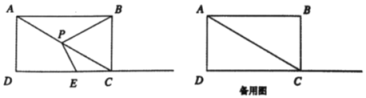
【题目】如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与A、C 重合),连接PB,过点P作PE⊥PB,交射线DC于点E,已知AD=3,sin∠BAC=![]() .设AP的长为x.
.设AP的长为x.
(1)AB等于多少;当x=1时,![]() 等于多少;
等于多少;
(2)①试探究: ![]() 否是定值?若是,请求出这个值;若不是,请说明理由;
否是定值?若是,请求出这个值;若不是,请说明理由;
②连接BE,设△PBE的面积为S,求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有三个班,其中九年一班和九年二班共有105名学生,在期末体育测试中,这两个班级共有79名学生满分,其中九年一班的满分率为70%,九年二班的满分率为80%.
(1)求九年一班和九年二班各有多少名学生.
(2)该校九年三班有45名学生,若九年级体育成绩的总满分率超过75%,求九年三班至少有多少名学生体育成绩是满分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=![]() AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的个数有( )
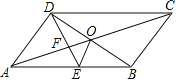
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。设公司一次性购买此型号笔记本电脑x合、
(I)根据题意,填写下表:

(II)设选择方案一的费用为y1元,选择方案二的费用为为y2元,分别写出y1,y2关于x的函数关系式;
(III)当x>15时,该公司采用哪种方案购买更合算?并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com