
某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
①甲队单独完成此项工程刚好如期完工;②乙队单独完成此项工程要比规定工期多用5天;③若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
如果工程不能按预定时间完工,公司每天将损失3000元,你觉得哪一种施工方案最节省工程款,并说明理由.
考点: 分式方程的应用.
专题: 工程问题.
分析: 先设甲队单独完成此项工程需x天,则乙队单独完成此项工程需(x+5)天,然后根据等量关系:甲乙合作4天的工作总量+乙做(规定天数﹣4)天的工作量=1列出分式方程,算出三种方案的价钱之后,再根据题意进行选择.
解答: 解:设甲队单独完成此项工程需x天,则乙队单独完成此项工程需(x+5)天.
依题意,得: =1,
=1,
解得:x=20.
经检验:x=20是原分式方程的解.
这三种施工方案需要的工程款为:
(1)1.5×20=30(万元);
(2)1.1×(20+5)+5×0.3=29(万元);
(3)1.5×4+1.1×20=28(万元).
综上所述,可知在保证正常完工的前提下,应选择第三种方案:即由甲、乙两队合作4天,剩下的工程由乙队独做.此时所需要的工程款最节省.
答:第三种方案:由甲、乙两队合作4天,剩下的工程由乙队独做.所需要的工程款最节省.
点评: 本题主要考查分式方程的应用,解题的关键是熟练掌握列分式方程解应用题的一般步骤,即①根据题意找出等量关系②列出方程③解出分式方程④检验⑤作答.注意:分式方程的解必须检验.


科目:初中数学 来源: 题型:
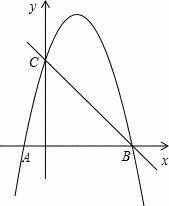
如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市5月上旬前5天的最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法错误的是( )
A. 平均数是30 B. 众数是29 C. 中位数是31 D. 极差是5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某天早晨王老师沿⊙M的半圆形M→A→B→M路径匀速散步,此时王老师离出发点M的距离y与时间x之间的函数关系的大致图象是( )
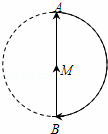
A.  B.
B. 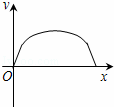 C.
C. 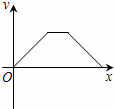 D.
D. 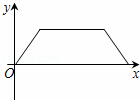
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com